
【題目】2016年上半年,股票投資人袁先生同時投資了甲、乙兩只股票,其中甲股票賺錢的概率為 ![]() ,賠錢的概率是
,賠錢的概率是 ![]() ;乙股票賺錢的概率為
;乙股票賺錢的概率為 ![]() ,賠錢的概率為
,賠錢的概率為 ![]() .對于甲股票,若賺錢則會賺取5萬元,若賠錢則損失4萬元;對于乙股票,若賺錢則會賺取6萬元,若賠錢則損失5萬元.
.對于甲股票,若賺錢則會賺取5萬元,若賠錢則損失4萬元;對于乙股票,若賺錢則會賺取6萬元,若賠錢則損失5萬元.
(Ⅰ)求袁先生2016年上半年同時投資甲、乙兩只股票賺錢的概率;
(Ⅱ)試求袁先生2016年上半年同事投資甲、乙兩只股票的總收益的分布列和數學期望.
【答案】解:(Ⅰ)袁先生2016年上半年同時投資甲、乙兩只股票賺錢的概率為:
p= ![]() =
= ![]() .
.
(Ⅱ)用X萬元表示袁先生2016年上半年同時投資甲、乙兩只股票的總收益,
則X所有可能取值為﹣9,0,2,11,
P(X=﹣9)= ![]() =
= ![]() ,
,
P(X=0)= ![]() =
= ![]() ,
,
P(X=2)= ![]() =
= ![]() ,
,
P(X=11)= ![]() =
= ![]() ,
,
∴X的分布列為:
X | ﹣9 | 0 | 2 | 11 |
P |
|
|
|
|
E(X)= ![]() =﹣
=﹣ ![]()
【解析】(Ⅰ)利用互斥事件概率加法公式和相互獨立事件概率乘法公式能求出袁先生2016年上半年同時投資甲、乙兩只股票賺錢的概率.(Ⅱ)用X萬元表示袁先生2016年上半年同時投資甲、乙兩只股票的總收益,則X所有可能取值為﹣9,0,2,11,分別求出相應的概率,由此能求出X的分布列和數學期望.
【考點精析】解答此題的關鍵在于理解離散型隨機變量及其分布列的相關知識,掌握在射擊、產品檢驗等例子中,對于隨機變量X可能取的值,我們可以按一定次序一一列出,這樣的隨機變量叫做離散型隨機變量.離散型隨機變量的分布列:一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn,X取每一個值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,則稱表為離散型隨機變量X 的概率分布,簡稱分布列.


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源: 題型:
【題目】拋物線![]() 的頂點為坐標原點O,焦點F在
的頂點為坐標原點O,焦點F在![]() 軸正半軸上,準線
軸正半軸上,準線![]() 與圓
與圓![]() 相切.
相切.
(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)已知直線![]() 和拋物線
和拋物線![]() 交于點
交于點![]() ,命題
,命題![]() :“若直線
:“若直線![]() 過定點(0,1),則
過定點(0,1),則 ![]() ”,
”,
請判斷命題![]() 的真假,并證明.
的真假,并證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】第 ![]() 屆夏季奧林匹克運動會將于2016年8月5日
屆夏季奧林匹克運動會將于2016年8月5日 ![]() 21日在巴西里約熱內盧舉行.下表是近五屆奧運會中國代表團和俄羅斯代表團獲得的金牌數的統計數據(單位:枚).
21日在巴西里約熱內盧舉行.下表是近五屆奧運會中國代表團和俄羅斯代表團獲得的金牌數的統計數據(單位:枚).
| 第31屆里約 | 第30屆倫敦 | 第29屆北京 | 第28屆雅典 | 第27屆悉尼 |
中國 | 26 | 38 | 51 | 32 | 28 |
俄羅斯 | 19 | 24 | 24 | 27 | 32 |
(1)根據表格中兩組數據完成近五屆奧運會兩國代表團獲得的金牌數的莖葉圖,并通過莖葉圖比較兩國代表團獲得的金牌數的平均值及分散程度(不要求計算出具體數值,給出結論即可);
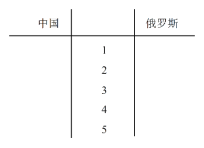
(2)下表是近五屆奧運會中國代表團獲得的金牌數之和 ![]() (從第
(從第 ![]() 屆算起,不包括之前已獲得的金牌數)隨時間
屆算起,不包括之前已獲得的金牌數)隨時間 ![]() (時間代號)變化的數據:
(時間代號)變化的數據:
屆 | 27 | 28 | 29 | 30 | 31 |
時間代號(x) | 1 | 2 | 3 | 5 | |
金牌數之和(y枚) | 28 | 60 | 111 | 149 | 175 |
作出散點圖如下:
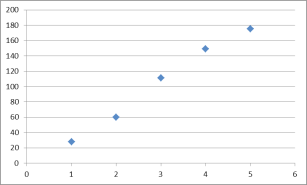
①由圖中可以看出,金牌數之和 ![]() 與時間代號
與時間代號 ![]() 之間存在線性相關關系,請求出
之間存在線性相關關系,請求出 ![]() 關于
關于 ![]() 的線性回歸方程;
的線性回歸方程;
②利用①中的回歸方程,預測2020年第32屆奧林匹克運動會中國代表團獲得的金牌數.
參考數據:![]() ,
,![]() ,
,![]() .
.
附:對于一組數據 ![]() ,
,![]() ,
,![]() ,
,![]() ,其回歸直線
,其回歸直線![]() 的斜率的最小二乘估計為
的斜率的最小二乘估計為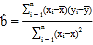 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】命題p:α∈R,sin(π﹣α)=cosα;命題q:“0<a<4”是“關于x的不等式ax2+ax+1>0的解集是實數集R”的充分必要條件,則下面結論正確的是( )
A.p是假命題
B.q是真命題
C.“p∧q”是假命題
D.“p∨q”是假命題
查看答案和解析>>
科目:高中數學 來源: 題型:
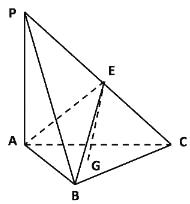
【題目】如圖,在三棱錐P﹣ABC中,平面PAC⊥平面ABC,PA⊥AC,AB=BC=CA=AP=2,G是△ABC重心,E是線段PC上一點,且CE=λCP.
(1)當EG∥平面PAB時,求λ的值;
(2)當直線CP與平面ABE所成角的正弦值為![]() 時,求λ的值.
時,求λ的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 上一點
上一點![]() 到其焦點
到其焦點![]() 的距離為4,橢圓
的距離為4,橢圓![]()
![]() 的離心率
的離心率![]() ,且過拋物線的焦點
,且過拋物線的焦點![]() .
.
(1)求拋物線![]() 和橢圓
和橢圓![]() 的標準方程;
的標準方程;
(2)過點![]() 的直線
的直線![]() 交拋物線
交拋物線![]() 于
于![]() 兩不同點,交
兩不同點,交![]() 軸于點
軸于點![]() ,已知
,已知![]() ,
, ![]() ,求證:
,求證: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圖是函數y=Asin(ωx+φ)(x∈R)在區間 ![]() 上的圖象,為了得到這個函數的圖象,只要將y=sinx(x∈R)的圖象上所有的點( )
上的圖象,為了得到這個函數的圖象,只要將y=sinx(x∈R)的圖象上所有的點( ) 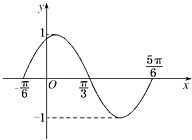
A.向左平移 ![]() 個單位長度,再把所得各點的橫坐標縮短到原來的
個單位長度,再把所得各點的橫坐標縮短到原來的 ![]() 倍,縱坐標不變
倍,縱坐標不變
B.向左平移 ![]() 個單位長度,再把所得各點的橫坐標伸長到原來的2倍,縱坐標不變
個單位長度,再把所得各點的橫坐標伸長到原來的2倍,縱坐標不變
C.向左平移 ![]() 個單位長度,再把所得各點的橫坐標縮短到原來的
個單位長度,再把所得各點的橫坐標縮短到原來的 ![]() 倍,縱坐標不變
倍,縱坐標不變
D.向左平移 ![]() 個單位長度,再把所得各點的橫坐標伸長到原來的2倍,縱坐標不變
個單位長度,再把所得各點的橫坐標伸長到原來的2倍,縱坐標不變
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l的參數方程為  (t為參數),曲線C的參數方程為
(t為參數),曲線C的參數方程為 ![]() (θ為參數)
(θ為參數)
(1)以原點O為極點,以x軸正半軸為極軸(與直角坐標系xOy取相同的長度單位)建立極坐標系,若點P的極坐標為(4, ![]() ),判斷點P與直線l的位置關系;
),判斷點P與直線l的位置關系;
(2)設點Q是曲線C上的一個動點,利用曲線C的參數方程求Q到直線l的距離的最大值與最小值的差.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com