
【題目】已知橢圓![]() :
:![]() ,
,![]() ,
,![]() 分別是橢圓短軸的上下兩個端點,
分別是橢圓短軸的上下兩個端點,![]() 是橢圓的左焦點,P是橢圓上異于點
是橢圓的左焦點,P是橢圓上異于點![]() ,
,![]() 的點,若
的點,若![]() 的邊長為4的等邊三角形.
的邊長為4的等邊三角形.
![]() 寫出橢圓的標準方程;
寫出橢圓的標準方程;
![]() 當直線
當直線![]() 的一個方向向量是
的一個方向向量是![]() 時,求以
時,求以![]() 為直徑的圓的標準方程;
為直徑的圓的標準方程;
![]() 設(shè)點R滿足:
設(shè)點R滿足:![]() ,
,![]() ,求證:
,求證:![]() 與
與![]() 的面積之比為定值.
的面積之比為定值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)證明見解析
;(3)證明見解析
【解析】
![]() 由
由![]() 是邊長為4的等邊三角形得
是邊長為4的等邊三角形得![]() ,進一步求得
,進一步求得![]() ,則橢圓方程可求;
,則橢圓方程可求;
![]() 由直線
由直線![]() 的一個方向向量是
的一個方向向量是![]() ,可得直線
,可得直線![]() 所在直線的斜率
所在直線的斜率![]() ,得到直線
,得到直線![]() 的方程,由橢圓方程聯(lián)立,求得P點坐標,得到
的方程,由橢圓方程聯(lián)立,求得P點坐標,得到![]() 的中點坐標,再求出
的中點坐標,再求出![]() ,可得以
,可得以![]() 為直徑的圓的半徑,則以
為直徑的圓的半徑,則以![]() 為直徑的圓的標準方程可求;
為直徑的圓的標準方程可求;
![]() 方法一、設(shè)
方法一、設(shè)![]() ,
,![]() 求出直線
求出直線![]() 的斜率,進一步得到直線
的斜率,進一步得到直線![]() 的斜率,得到直線
的斜率,得到直線![]() 的方程,同理求得直線
的方程,同理求得直線![]() 的方程,聯(lián)立兩直線方程求得R的橫坐標,再結(jié)合
的方程,聯(lián)立兩直線方程求得R的橫坐標,再結(jié)合![]() 在橢圓
在橢圓![]() 上可得
上可得![]() 與
與![]() 的關(guān)系,由
的關(guān)系,由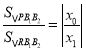 求解;
求解;
方法二、設(shè)直線![]() ,
,![]() 的斜率為k,得直線
的斜率為k,得直線![]() 的方程為
的方程為![]() 結(jié)合
結(jié)合![]() ,可得直線
,可得直線![]() 的方程為
的方程為![]() ,把
,把![]() 與橢圓方程聯(lián)立可得
與橢圓方程聯(lián)立可得![]() ,再由
,再由![]() 在橢圓
在橢圓![]() 上,得到
上,得到![]() ,從而得到
,從而得到![]() ,得
,得![]() 結(jié)合
結(jié)合![]() ,可得直線
,可得直線![]() 的方程為
的方程為![]() 與線
與線![]() 的方程聯(lián)立求得
的方程聯(lián)立求得![]() 再由
再由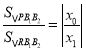 求解.
求解.
![]() 解:如圖,由
解:如圖,由![]() 的邊長為4的等邊三角形,得
的邊長為4的等邊三角形,得![]() ,且
,且![]() .
.

![]() 橢圓的標準方程為
橢圓的標準方程為![]() ;
;
![]() 解:
解:![]() 直線
直線![]() 的一個方向向量是
的一個方向向量是![]() ,
,
![]() 直線
直線![]() 所在直線的斜率
所在直線的斜率![]() ,則直線
,則直線![]() 的方程為
的方程為![]() ,
,
聯(lián)立 ,得
,得![]() ,
,
解得![]() ,
,![]() .
.
則![]() 的中點坐標為
的中點坐標為![]() ,
,![]() .
.
則以![]() 為直徑的圓的半徑
為直徑的圓的半徑![]() .
.
![]() 以
以![]() 為直徑的圓的標準方程為
為直徑的圓的標準方程為![]() ;
;
![]() 證明:方法一、設(shè)
證明:方法一、設(shè)![]() ,
,![]()
直線![]() 的斜率為
的斜率為![]() ,由
,由![]() ,得直線
,得直線![]() 的斜率為
的斜率為![]() .
.
于是直線![]() 的方程為:
的方程為:![]() .
.
同理,![]() 的方程為:
的方程為:![]() .
.
聯(lián)立兩直線方程,消去y,得![]() .
.
![]() 在橢圓
在橢圓![]() 上,
上,
![]() ,從而
,從而![]() .
.
![]() ,
,
 .
.
方法二、設(shè)直線![]() ,
,![]() 的斜率為k,
的斜率為k,![]() ,則直線
,則直線![]() 的方程為
的方程為![]() .
.
由![]() ,直線
,直線![]() 的方程為
的方程為![]() ,
,
將![]() 代入
代入![]() ,得
,得![]() ,
,
![]() 是橢圓上異于點
是橢圓上異于點![]() ,
,![]() 的點,
的點,![]() ,從而
,從而![]() .
.
![]() 在橢圓
在橢圓![]() 上,
上,
![]() ,從而
,從而![]() .
.
![]() ,得
,得![]() .
.
![]() ,
,![]() 直線
直線![]() 的方程為
的方程為![]() .
.
聯(lián)立 ,解得
,解得![]() ,即
,即![]() .
.
 .
.


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖,在多面體![]() 中,四邊形
中,四邊形![]() 是矩形,
是矩形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.

(1)若![]() 點是
點是![]() 的中點,求證:
的中點,求證:![]() 平面
平面![]() ;
;
(2)求證:平面![]() 平面
平面![]() ;
;
(3)若![]() ,求直線
,求直線![]() 與平面
與平面![]() 成角的正弦值.
成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某班隨機抽查了![]() 名學生的數(shù)學成績,分數(shù)制成如圖的莖葉圖,其中
名學生的數(shù)學成績,分數(shù)制成如圖的莖葉圖,其中![]() 組學生每天學習數(shù)學時間不足
組學生每天學習數(shù)學時間不足![]() 個小時,
個小時,![]() 組學生每天學習數(shù)學時間達到一個小時,學校規(guī)定
組學生每天學習數(shù)學時間達到一個小時,學校規(guī)定![]() 分及
分及![]() 分以上記為優(yōu)秀,
分以上記為優(yōu)秀,![]() 分及
分及![]() 分以上記為達標,
分以上記為達標,![]() 分以下記為未達標.
分以下記為未達標.

(1)根據(jù)莖葉圖完成下面的列聯(lián)表:
達標 | 未達標 | 總計 | |
| |||
| |||
總計 |
(2)判斷是否有![]() 的把握認為“數(shù)學成績達標與否”與“每天學習數(shù)學時間能否達到一小時”有關(guān).
的把握認為“數(shù)學成績達標與否”與“每天學習數(shù)學時間能否達到一小時”有關(guān).
參考公式與臨界值表: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】過年時小明的舅舅在家庭微信群里發(fā)了一個10元的紅包,紅包被隨機分配為2.51元,3.32元,1.24元,0.26元,2.67元,共五份.現(xiàn)已知小明與爸爸都各自搶到了一個紅包,則兩人搶到紅包的金額總和不小于4元的概率為__________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某學校為鼓勵家校互動,與某手機通訊商合作,為教師辦理流量套餐.為了解該校教師手機流量使用情況,通過抽樣,得到![]() 位教師近
位教師近![]() 年每人手機月平均使用流量
年每人手機月平均使用流量![]() (單位:
(單位:![]() )的數(shù)據(jù),其頻率分布直方圖如下:
)的數(shù)據(jù),其頻率分布直方圖如下:

若將每位教師的手機月平均使用流量分別視為其手機月使用流量,并將頻率為概率,回答以下問題.
(Ⅰ) 從該校教師中隨機抽取![]() 人,求這
人,求這![]() 人中至多有
人中至多有![]() 人月使用流量不超過
人月使用流量不超過![]()
![]() 的概率;
的概率;
(Ⅱ) 現(xiàn)該通訊商推出三款流量套餐,詳情如下:
套餐名稱 | 月套餐費(單位:元) | 月套餐流量(單位: |
|
|
|
|
|
|
|
|
|
這三款套餐都有如下附加條款:套餐費月初一次性收取,手機使用一旦超出套餐流量,系統(tǒng)就自動幫用戶充值![]()
![]() 流量,資費
流量,資費![]() 元;如果又超出充值流量,系統(tǒng)就再次自動幫用戶充值
元;如果又超出充值流量,系統(tǒng)就再次自動幫用戶充值![]()
![]() 流量,資費
流量,資費![]() 元/次,依次類推,如果當月流量有剩余,系統(tǒng)將自動清零,無法轉(zhuǎn)入次月使用.
元/次,依次類推,如果當月流量有剩余,系統(tǒng)將自動清零,無法轉(zhuǎn)入次月使用.
學校欲訂購其中一款流量套餐,為教師支付月套餐費,并承擔系統(tǒng)自動充值的流量資費的![]() ,其余部分由教師個人承擔,問學校訂購哪一款套餐最經(jīng)濟?說明理由.
,其余部分由教師個人承擔,問學校訂購哪一款套餐最經(jīng)濟?說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】“割圓術(shù)”是劉徽最突出的數(shù)學成就之一,他在《九章算術(shù)注》中提出割圓術(shù),并作為計算圓的周長,面積已經(jīng)圓周率的基礎(chǔ),劉徽把圓內(nèi)接正多邊形的面積一直算到了正3072邊形,并由此而求得了圓周率為3.1415和3.1416這兩個近似數(shù)值,這個結(jié)果是當時世界上圓周率計算的最精確數(shù)據(jù).如圖,當分割到圓內(nèi)接正六邊形時,某同學利用計算機隨機模擬法向圓內(nèi)隨機投擲點,計算得出該點落在正六邊形內(nèi)的頻率為0.8269,那么通過該實驗計算出來的圓周率近似值為(參考數(shù)據(jù):![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 的圖象過點
的圖象過點![]() ,且在點
,且在點![]() 處的切線與直線
處的切線與直線![]() 平行.
平行.
(1)求實數(shù)![]() ,
,![]() 的值;
的值;
(2)若對任意的![]() ,函數(shù)
,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上總不是單調(diào)函數(shù),求實數(shù)
上總不是單調(diào)函數(shù),求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】一商家誠邀甲、乙兩名圍棋高手進行一場網(wǎng)絡(luò)國棋比賽,每比賽一局商家要向每名棋手支付2000元對局費,同時商家每局從轉(zhuǎn)讓網(wǎng)絡(luò)轉(zhuǎn)播權(quán)及廣告宣傳中獲利12100元,從兩名棋手以往比賽中得知,甲每局獲勝的概率為![]() ,乙每局獲勝的概率為
,乙每局獲勝的概率為![]() ,兩名棋手約定:最多下五局,先連勝兩局者獲勝,比賽結(jié)束,比賽結(jié)束后,商家為獲勝者頒發(fā)5000元的獎金,若沒有決出獲勝者則各頒發(fā)2500元.
,兩名棋手約定:最多下五局,先連勝兩局者獲勝,比賽結(jié)束,比賽結(jié)束后,商家為獲勝者頒發(fā)5000元的獎金,若沒有決出獲勝者則各頒發(fā)2500元.
(1)求下完五局且甲獲勝的概率是多少;
(2)求商家從這場網(wǎng)絡(luò)棋賽中獲得的收益的數(shù)學期望是多少.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com