
【題目】一商家誠邀甲、乙兩名圍棋高手進行一場網絡國棋比賽,每比賽一局商家要向每名棋手支付2000元對局費,同時商家每局從轉讓網絡轉播權及廣告宣傳中獲利12100元,從兩名棋手以往比賽中得知,甲每局獲勝的概率為![]() ,乙每局獲勝的概率為
,乙每局獲勝的概率為![]() ,兩名棋手約定:最多下五局,先連勝兩局者獲勝,比賽結束,比賽結束后,商家為獲勝者頒發5000元的獎金,若沒有決出獲勝者則各頒發2500元.
,兩名棋手約定:最多下五局,先連勝兩局者獲勝,比賽結束,比賽結束后,商家為獲勝者頒發5000元的獎金,若沒有決出獲勝者則各頒發2500元.
(1)求下完五局且甲獲勝的概率是多少;
(2)求商家從這場網絡棋賽中獲得的收益的數學期望是多少.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根據題意,連勝兩局獲勝.若比賽五局,且甲獲勝,則五局的勝負情況為乙勝,甲勝,乙勝,甲勝,甲勝.進而由各自取勝的概率即可求解.
(2)根據題意可知,兩人比賽局數![]() 可能的取值有
可能的取值有![]() .由所給取勝的概率,分別求得這四種情況下的概率,即可求得比賽局數的期望.扣除支出,即為商家獲得的收益情況.
.由所給取勝的概率,分別求得這四種情況下的概率,即可求得比賽局數的期望.扣除支出,即為商家獲得的收益情況.
(1)根據題意,先連勝兩局者獲勝.則下完五局甲獲勝,這五局的勝負情況分別為:
乙勝,甲勝,乙勝,甲勝,甲勝.
甲每局獲勝的概率為![]() ,乙每局獲勝的概率為
,乙每局獲勝的概率為![]()
所以下完五局甲獲勝的概率為![]()
(2)設![]() 為比賽的局數,
為比賽的局數,![]() 表示商家獲得的收益
表示商家獲得的收益
則![]()
由題意可知,![]() 可能的取值有
可能的取值有![]()
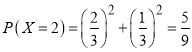
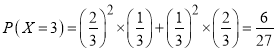
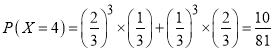
當比賽五局時,前四局兩人各勝兩局,且第五局無論誰勝商家都需支付5000元,因而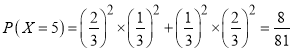
所以由離散型數學期望公式可得![]()
故![]()
所以商家從這場網絡棋賽中獲得的收益的數學期望是![]()


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2-mlnx,h(x)=x2-x+a.
(1)當a=0時,f(x)≥h(x)在(1,+∞)上恒成立,求實數m的取值范圍;
(2)當m=2時,若函數k(x)=f(x)-h(x)在區間(1,3)上恰有兩個不同零點,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某船由甲地逆水行駛到乙地,甲、乙兩地相距s(km),水的流速為常量a(![]() ),船在靜水中的最大速度為b(
),船在靜水中的最大速度為b(![]() )(
)(![]() ),已知船每小時的燃料費用(以元為單位)與船在靜水中的速度的平方成正比,比例系數為k,則船在靜水中的航行速度為多少時,其全程的燃料費用最省?
),已知船每小時的燃料費用(以元為單位)與船在靜水中的速度的平方成正比,比例系數為k,則船在靜水中的航行速度為多少時,其全程的燃料費用最省?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年初,我國突發新冠肺炎疫情.面對“突發災難”,舉國上下心,繼解放軍醫療隊于除夕夜飛抵武漢,各省醫療隊也陸續增援,紛紛投身疫情防控與病人救治之中.為分擔“逆行者”的后顧之憂,某大學學生志愿者團隊開展“愛心輔學”活動,為抗疫前線工作者子女在線輔導功課.現隨機安排甲、乙、丙3名志愿者為某學生輔導數學、物理、化學、生物4門學科,每名志愿者至少輔導1門學科,每門學科由1名志愿者輔導,則數學學科恰好由甲輔導的概率為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圓周上有800個點,依順時針方向標號為![]() ,它們將圓周分成800個間隙.今選定某一點染成紅色,然后按如下規則,逐次染紅其余的一些點:如果第
,它們將圓周分成800個間隙.今選定某一點染成紅色,然后按如下規則,逐次染紅其余的一些點:如果第![]() 號點已被染紅,則可按順時針方向轉過
號點已被染紅,則可按順時針方向轉過![]() 個間隙,再將所到達的那個端點染紅.如此繼續下去.試問圓周上最多可得到多少個紅點?證明你的結論.
個間隙,再將所到達的那個端點染紅.如此繼續下去.試問圓周上最多可得到多少個紅點?證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有四名男生,三名女生排隊照相,七個人排成一排,則下列說法正確的有( )
A.如果四名男生必須連排在一起,那么有![]() 種不同排法
種不同排法
B.如果三名女生必須連排在一起,那么有![]() 種不同排法
種不同排法
C.如果女生不能站在兩端,那么有![]() 種不同排法
種不同排法
D.如果三個女生中任何兩個均不能排在一起,那么有![]() 種不同排法
種不同排法
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在梯形![]() 中(圖1),
中(圖1),![]() ,
, ![]() ,
, ![]() ,過
,過![]() 、
、![]() 分別作
分別作![]() 的垂線,垂足分別為
的垂線,垂足分別為![]() 、
、![]() ,已知
,已知![]() ,
, ![]() ,將梯形
,將梯形![]() 沿
沿![]() 、
、![]() 同側折起,使得
同側折起,使得![]() ,
, ![]() ,得空間幾何體
,得空間幾何體![]() (圖2).
(圖2).
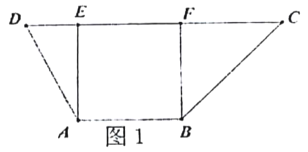
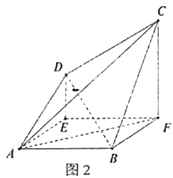
(1)證明: ![]() 平面
平面![]() ;
;
(2)求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是中國古代的數學專著,其中的“更相減損術”可以用來求兩個數的最大公約數,原文是:可半者半之,不可半者,副置分母、子之數,以少減多,更相減損,求其等也,以等數約之. 翻譯為現代的語言如下:如果需要對分數進行約分,那么可以折半的話,就折半(也就是用2來約分).如果不可以折半的話,那么就比較分母和分子的大小,用大數減去小數,互相減來減去,一直到減數與差相等為止,用這個相等的數字來約分,現給出“更相減損術”的程序框圖如圖所示,如果輸入的![]() ,
,![]() ,則輸出的
,則輸出的![]() ( )
( )
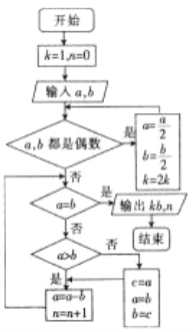
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com