
【題目】已知函數![]() ,
,![]() .
.
(1)當![]() 時,求曲線
時,求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)當![]() 時,求函數
時,求函數![]() 的最小值;
的最小值;
(3)已知![]() ,且任意
,且任意![]() 有
有![]() ,求實數a的取值范圍.
,求實數a的取值范圍.
【答案】(1)![]() ;(2)分類討論,詳見解析;(3)
;(2)分類討論,詳見解析;(3)![]() .
.
【解析】
(1)當x>1時,f(x)=x3+3x﹣3,f(2)=11.由f'(x)=3x2+3,得f'(2)=15.由此利用導數的幾何意義能求出y=f(x)在x=2處的切線方程;
(2)當a≤﹣1時,得f(x)=x3+3x﹣3a,由f'(x)=3x2+3>0,得到f(x)min=f(﹣1)=﹣4﹣3a.當a≥1時,得f(x)=x3﹣3x+3a,由f'(x)=3x2﹣3≤0,得到f(x)min=f(1)=﹣2+3a.當﹣1<a<1時,f(x) ,由此能求出函數f(x)的最小值;
,由此能求出函數f(x)的最小值;
(3)當a>0,且任意x≥1有f(x+a)﹣f(1+a)≥15a2lnx,即對任意x≥1有(x+a)3+3x﹣15a2lnx﹣(a+1)3﹣3≥0.設g(x)=(x+a)3+3x﹣15a2lnx﹣(a+1)3﹣3,則g(1)=0,g'(x)=3(x+a)2+3![]() .設h(x)=g'(x)=3(x+a)2+3
.設h(x)=g'(x)=3(x+a)2+3![]() ,則h'(x)=6(x+a)
,則h'(x)=6(x+a)![]() 0,由此利用導數性質能求出結果.
0,由此利用導數性質能求出結果.
解:(1)當![]() 時,
時,![]() ,
,![]() .由
.由![]() ,得
,得![]() .
.
所以![]() 在
在![]() 處的切線方程為
處的切線方程為![]() 即
即![]() .
.
(2)①當![]() 時,得
時,得![]() ,因為
,因為![]() ,
,
所以![]() 在
在![]() 單調遞增,所以
單調遞增,所以![]() .
.
②當![]() 時,得
時,得![]() ,因為
,因為![]() ,
,
所以![]() 在
在![]() 單調遞減,所以
單調遞減,所以![]() .
.
③當![]() 時,
時,
由①②知:函數![]() 在
在![]() 單調遞減,
單調遞減,![]() 單調遞增,所以
單調遞增,所以![]() ,
,
綜上,當![]() ,
,![]() ;
;
當![]() 時,
時,![]() ;
;
當![]() 時,
時,![]() .
.
(3)當![]() ,且任意
,且任意![]() 有
有![]() ,
,
即對任意![]() 有
有![]() .
.
設![]() ,
,
則![]() ,
,![]() .
.
設![]() ,
,
因為![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 單調遞增,
單調遞增,
所以![]() ,即
,即![]() ,
,
①當![]() 即
即![]() 時,所以
時,所以![]() 恒成立,
恒成立,
所以![]() 在
在![]() 單調遞增,此時
單調遞增,此時![]() ,滿足題意.
,滿足題意.
②當![]() 即
即![]() 時,
時,
因為![]() ,且
,且![]() 在
在![]() 單調遞增,
單調遞增,
所以存在唯一的![]() ,使得
,使得![]() ,
,
因此當![]() 時
時![]() ;當
;當![]() 時
時![]() ;
;
所以![]() 在
在![]() 單調遞減,
單調遞減,![]() 單調遞增.
單調遞增.
所以![]() ,不滿足題意.
,不滿足題意.
綜上,![]() .
.


 培優口算題卡系列答案
培優口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案科目:高中數學 來源: 題型:
【題目】如圖,在底面為直角梯形的四棱錐P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,PA=3,AD=2,AB=2![]() ,BC=6.
,BC=6.
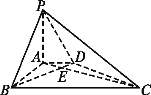
(1)求證:BD⊥平面PAC; (2)求二面角P-BD-A的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,直角坐標系中,圓的方程為![]() ,
,![]() ,
,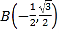 ,
,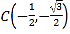 為圓上三個定點,某同學從
為圓上三個定點,某同學從![]() 點開始,用擲骰子的方法移動棋子.規定:①每擲一次骰子,把一枚棋子從一個定點沿圓弧移動到相鄰下一個定點;②棋子移動的方向由擲骰子決定,若擲出骰子的點數為偶數,則按圖中箭頭方向移動;若擲出骰子的點數為奇數,則按圖中箭頭相反的方向移動.設擲骰子
點開始,用擲骰子的方法移動棋子.規定:①每擲一次骰子,把一枚棋子從一個定點沿圓弧移動到相鄰下一個定點;②棋子移動的方向由擲骰子決定,若擲出骰子的點數為偶數,則按圖中箭頭方向移動;若擲出骰子的點數為奇數,則按圖中箭頭相反的方向移動.設擲骰子![]() 次時,棋子移動到
次時,棋子移動到![]() ,
,![]() ,
,![]() 處的概率分別為
處的概率分別為![]() ,
,![]() ,
,![]() .例如:擲骰子一次時,棋子移動到
.例如:擲骰子一次時,棋子移動到![]() ,
,![]() ,
,![]() 處的概率分別為
處的概率分別為![]() ,
,![]() ,
,![]() .
.
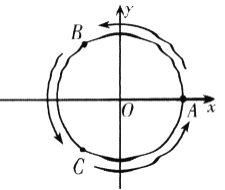
(1)分別擲骰子二次,三次時,求棋子分別移動到![]() ,
,![]() ,
,![]() 處的概率;
處的概率;
(2)擲骰子![]() 次時,若以
次時,若以![]() 軸非負半軸為始邊,以射線
軸非負半軸為始邊,以射線![]() ,
,![]() ,
,![]() 為終邊的角的余弦值記為隨機變量
為終邊的角的余弦值記為隨機變量![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
(3)記![]() ,
,![]() ,
,![]() ,其中
,其中![]() .證明:數列
.證明:數列![]() 是等比數列,并求
是等比數列,并求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】過拋物線C:x2=4y的準線上任意一點P作拋物線的切線PA,PB,切點分別為A,B,則A點到準線的距離與B點到準線的距離之和的最小值是( )
A.7B.6C.5D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在坐標原點,焦點在
的中心在坐標原點,焦點在![]() 軸上,左頂點為
軸上,左頂點為![]() ,左焦點為
,左焦點為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,直線
上,直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,直線
兩點,直線![]() ,
, ![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,
, ![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)以![]() 為直徑的圓是否經過定點?若經過,求出定點的坐標;若不經過,請說明理由.
為直徑的圓是否經過定點?若經過,求出定點的坐標;若不經過,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年是五四運動100周年.五四運動以來的100年,是中國青年一代又一代接續奮斗、凱歌前行的100年,是中口青年用青春之我創造青春之中國、青春之民族的100年.為繼承和發揚五四精神在青年節到來之際,學校組織“五四運動100周年”知識競賽,競賽的一個環節由10道題目組成,其中6道A類題、4道B類題,參賽者需從10道題目中隨機抽取3道作答,現有甲同學參加該環節的比賽.
(1)求甲同學至少抽到2道B類題的概率;
(2)若甲同學答對每道A類題的概率都是![]() ,答對每道B類題的概率都是
,答對每道B類題的概率都是![]() ,且各題答對與否相互獨立.現已知甲同學恰好抽中2道A類題和1道B類題,用X表示甲同學答對題目的個數,求隨機變量X的分布列和數學期望.
,且各題答對與否相互獨立.現已知甲同學恰好抽中2道A類題和1道B類題,用X表示甲同學答對題目的個數,求隨機變量X的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com