
【題目】已知函數![]() ,
, ![]() 為常數.
為常數.
(![]() )若
)若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
(![]() )若對任意的
)若對任意的![]() 都有不等式
都有不等式![]() 成立,求
成立,求![]() 的值.
的值.
(![]() )在(
)在(![]() )的條件下,若函數
)的條件下,若函數![]() 的圖像與
的圖像與![]() 軸恰有三個相異的公共點,求實數
軸恰有三個相異的公共點,求實數![]() 的取值范圍.
的取值范圍.
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ;(
;(![]() )
)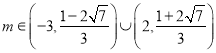 .
.
【解析】試題分析:(1)對二次項系數進行討論,分為![]() 符合題意,
符合題意, ![]() 時,根據為此函數的性質可得不合題意,
時,根據為此函數的性質可得不合題意, ![]() 時,解一元二次不等式可得結果;(2)根據一元二次不等式的性質可得
時,解一元二次不等式可得結果;(2)根據一元二次不等式的性質可得![]() 時,不合題意,故應
時,不合題意,故應![]() ,
, ![]() ,從而可解出
,從而可解出![]() ;(3)結合(2)中的結果將其利用分段函數進行表達
;(3)結合(2)中的結果將其利用分段函數進行表達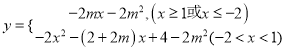 ,根據一次函數的性質可得
,根據一次函數的性質可得![]() 必有一根,解出方程得
必有一根,解出方程得![]() ,根據二次函數的性質可得
,根據二次函數的性質可得![]() 必有兩個不等根,利用數形結合思想得
必有兩個不等根,利用數形結合思想得![]() ,綜合可得最后結果.
,綜合可得最后結果.
試題解析:(![]() )當
)當![]() 時,
時, ![]() 時,
時, ![]() ,符合;
,符合;
當![]() 時,開口向下,在
時,開口向下,在![]() 上不能恒正,舍;
上不能恒正,舍;
當![]() 時,
時, ![]() ,
,
解得: ![]() 或
或![]() ,符合;綜上:
,符合;綜上: ![]() 的范圍是
的范圍是![]() .
.
(![]() )
)![]() ,
, ![]() ,對
,對![]() 恒成立,
恒成立,
當![]() 時,
時, ![]() ,不合題意(舍);當
,不合題意(舍);當![]() 時,不合題意(舍);當
時,不合題意(舍);當![]() 時,
時, ![]() ,即
,即![]() ,∴綜上:
,∴綜上: ![]() .
.
(![]() )
)![]() ,
,
∴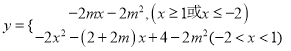 ,
,
則![]() ,必有一根,
,必有一根, ![]() ,
, ![]() 或
或![]() ,
,
![]() ,必有兩個不等根,
,必有兩個不等根,
∴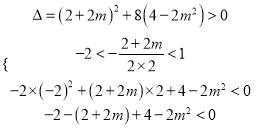 ,得
,得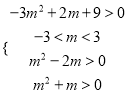 ,
,
綜上: ![]() 范圍
范圍 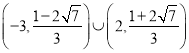 .
.


 沖刺100分1號卷系列答案
沖刺100分1號卷系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() .
. ![]() 在
在![]() 上有最大值9,最小值4.
上有最大值9,最小值4.
(1)求實數![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)若方程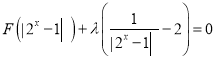 有三個不同的實數根,求實數
有三個不同的實數根,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“a=﹣1”是“直線ax+3y+2=0與直線x+(a﹣2)y+1=0平行”的( )
A.充分不必要條件
B.必要不充分條件
C.充要條件
D.既不充分也不必要條件
查看答案和解析>>
科目:高中數學 來源: 題型:
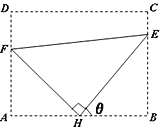
【題目】如圖,某污水處理廠要在一個矩形污水處理池![]() 的池底水平鋪設污水凈化管道(
的池底水平鋪設污水凈化管道(![]() ,
, ![]() 是直角頂點)來處理污水,管道越長,污水凈化效果越好.設計要求管道的接口
是直角頂點)來處理污水,管道越長,污水凈化效果越好.設計要求管道的接口![]() 是
是![]() 的中點,
的中點, ![]() 分別落在線段
分別落在線段![]() 上.已知
上.已知![]() 米,
米, ![]() 米,記
米,記![]() .
.
(1)試將污水凈化管道的總長度![]() (即
(即![]() 的周長)表示為
的周長)表示為![]() 的函數,并求出定義域;
的函數,并求出定義域;
(2)問![]() 當取何值時,污水凈化效果最好?并求出此時管道的總長度.
當取何值時,污水凈化效果最好?并求出此時管道的總長度.
(提示: ![]() .)
.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設正三棱錐A﹣BCD(底面是正三角形,頂點在底面的射影為底面中心)的所有頂點都在球O的球面上,BC=2,E,F分別是AB,BC的中點,EF⊥DE,則球O的表面積為( )
A.![]()
B.6π
C.8π
D.12π
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() .(14分)
.(14分)
(1)此方程表示圓,求m的取值范圍;
(2)若(1)中的圓與直線x+2y-4=0相交于M、N兩點,且![]() (O為坐標原點),求m的值;
(O為坐標原點),求m的值;
(3)在(2)的條件下,求以![]() 為直徑的圓的方程.
為直徑的圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法中,正確的個數是( )
①函數f(x)=2x﹣x2的零點有2個;
②函數y=sin(2x+ ![]() )sin(
)sin( ![]() ﹣2x)的最小正周期是π;
﹣2x)的最小正周期是π;
③命題“函數f(x)在x=x0處有極值,則f′(x0)=0”的否命題是真命題;
④ ![]() dx=
dx= ![]() .
.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,設二次函數
中,設二次函數![]() 的圖像與兩坐標軸有三個交點,經過這三點的圓記為
的圖像與兩坐標軸有三個交點,經過這三點的圓記為![]()
(1)求圓![]() 的方程;
的方程;
(2)若過點![]() 的直線
的直線![]() 與圓
與圓![]() 相交,所截得的弦長為4,求直線
相交,所截得的弦長為4,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com