
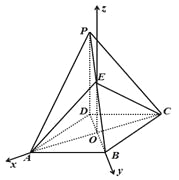
【題目】(本題滿分14分)如圖,在四棱錐![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 是菱形,
是菱形, ![]() ,
, ![]() 為
為![]() 與
與![]() 的交點,
的交點, ![]() 為
為![]() 上任意一點.
上任意一點.

(1)證明:平面![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,并且二面角
,并且二面角![]() 的大小為
的大小為![]() ,求
,求![]() 的值.
的值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】試題分析:(1)解決立體幾何的有關問題,空間想象能力是非常重要的,但新舊知識的遷移融合也很重要,在平面幾何的基礎上,把某些空間問題轉化為平面問題來解決,有時很方便;(2)證明兩個平面垂直,首先考慮直線與平面垂直,也可以簡單記為“證面面垂直,找線面垂直”,是化歸思想的體現,這種思想方法與空間中的平行關系的證明類似,掌握化歸與轉化思想方法是解決這類題的關鍵;(3)空間向量將空間位置關系轉化為向量運算,應用的核心是要充分認識形體特征,建立恰當的坐標系,實施幾何問題代數化.同時注意兩點:一是正確寫出點、向量的坐標,準確運算;二是空間位置關系中判定定理與性質定理條件要完備.
試題解析:(1)因為![]() ,
, ![]() ,
,
又![]() 是菱形,
是菱形, ![]() ,故
,故![]() 平面
平面![]()
![]() 平面
平面![]() 平面
平面![]() 4分
4分
(2)連結![]() ,因為
,因為![]() 平面
平面![]() ,
,
所以![]() ,所以
,所以![]() 平面
平面![]()
又![]() 是
是![]() 的中點,故此時
的中點,故此時![]() 為
為![]() 的中點,
的中點,
以![]() 為坐標原點,射線
為坐標原點,射線![]() 分別為
分別為![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸建立空間直角坐標系. .6分
軸建立空間直角坐標系. .6分
設![]() 則
則![]() ,
,
![]()
向量![]() 為平面
為平面![]() 的一個法向量 .8分
的一個法向量 .8分
設平面![]() 的一個法向量
的一個法向量![]() ,
,
則![]() 且
且![]() ,
,
即![]() ,
,
取![]() ,則
,則![]() ,則
,則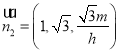 12分
12分
 解得
解得![]()
故![]() 14分
14分


科目:高中數學 來源: 題型:
【題目】橢圓C焦點在y軸上,離心率為 ![]() ,上焦點到上頂點距離為2﹣
,上焦點到上頂點距離為2﹣ ![]() .
.
(1)求橢圓C的標準方程;
(2)直線l與橢圓C交與P,Q兩點,O為坐標原點,△OPQ的面積S△OPQ=1,則| ![]() |2+|
|2+| ![]() |2是否為定值,若是求出定值;若不是,說明理由.
|2是否為定值,若是求出定值;若不是,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=cos4x﹣2sinxcosx﹣sin4x.
(1)求f(x)的最小正周期;
(2)求f(x)的單調增區間;
(3)若 ![]() ,求f(x)的值域.
,求f(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據以往的經驗,某工程施工期間的將數量X(單位:mm)對工期的影響如下表:
降水量X | X<300 | 300≤X<700 | 700≤X<900 | X≥900 |
工期延誤天數Y | 0 | 2 | 6 | 10 |
歷年氣象資料表明,該工程施工期間降水量X小于300,700,900的概率分別為0.3,0.7,0.9,求:
(1)工期延誤天數Y的均值與方差;
(2)在降水量X至少是300的條件下,工期延誤不超過6天的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com