
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為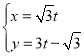 (
(![]() 為參數(shù)),以坐標(biāo)原點為極點,
為參數(shù)),以坐標(biāo)原點為極點,![]() 軸的非負(fù)半軸為極軸且取相同的單位長度建立極坐標(biāo)系,曲線
軸的非負(fù)半軸為極軸且取相同的單位長度建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求直線![]() 的極坐標(biāo)方程和曲線
的極坐標(biāo)方程和曲線![]() 的參數(shù)方程;
的參數(shù)方程;
(2)若![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
【答案】(1)![]() ;
; (
(![]() 為參數(shù));(2)
為參數(shù));(2)![]()
【解析】
(1)先將直線![]() 的參數(shù)方程消去參數(shù)
的參數(shù)方程消去參數(shù)![]() 化為普通方程,再直角坐標(biāo)方程與極坐標(biāo)方程的互化公式,即求出直線
化為普通方程,再直角坐標(biāo)方程與極坐標(biāo)方程的互化公式,即求出直線![]() 的極坐標(biāo)方程;同樣由直角坐標(biāo)方程與極坐標(biāo)方程的互化公式,先將曲線
的極坐標(biāo)方程;同樣由直角坐標(biāo)方程與極坐標(biāo)方程的互化公式,先將曲線![]() 的極坐標(biāo)方程化為直角坐標(biāo)方程,進(jìn)而可求出曲線
的極坐標(biāo)方程化為直角坐標(biāo)方程,進(jìn)而可求出曲線![]() 的參數(shù)方程;
的參數(shù)方程;
(2)求出直線![]() 的參數(shù)方程的標(biāo)準(zhǔn)形式,然后利用參數(shù)
的參數(shù)方程的標(biāo)準(zhǔn)形式,然后利用參數(shù)![]() 的幾何意義,即可求出
的幾何意義,即可求出![]() 的值.
的值.
(1)依題意,得直線![]() ,即
,即![]() ,
,
所以直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
因為![]() ,則
,則![]() ,即
,即![]() .
.
所以曲線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)).
為參數(shù)).
(2)因為直線![]() 經(jīng)過點
經(jīng)過點![]() ,
,
故直線![]() 的參數(shù)方程的標(biāo)準(zhǔn)形式為
的參數(shù)方程的標(biāo)準(zhǔn)形式為 ,代入
,代入![]() ,
,
可得![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (其中e是自然對數(shù)的底數(shù),a,
(其中e是自然對數(shù)的底數(shù),a,![]() )在點
)在點![]() 處的切線方程是
處的切線方程是![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間.
的單調(diào)區(qū)間.
(2)設(shè)函數(shù)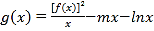 ,若
,若![]() 在
在![]() 上恒成立,求實數(shù)m的取值范圍.
上恒成立,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點![]() ,
,![]() 是橢圓
是橢圓![]() 的左,右焦點,橢圓上一點
的左,右焦點,橢圓上一點![]() 滿足
滿足![]() 軸,
軸,![]() ,
,![]() .
.
(1)求橢圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)過![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,當(dāng)
兩點,當(dāng)![]() 的內(nèi)切圓面積最大時,求直線
的內(nèi)切圓面積最大時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(I) 當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(II) 當(dāng)![]() 時,
時,![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2013年華人數(shù)學(xué)家張益唐證明了孿生素數(shù)猜想的一個弱化形式,此事引起了國際數(shù)學(xué)界的轟動許多專家認(rèn)為這是數(shù)論研究中的一項重大突破世界主流媒體都對這項重要成果作了報道并給予了高度評價,印度媒體甚至稱贊張益唐為“中國的拉馬努金”.孿生素數(shù)猜想是希爾伯特在1900年提出的23個問題之一,可以這樣描述:存在無窮多個素數(shù)![]() ,使得
,使得![]() 是素數(shù),素數(shù)對
是素數(shù),素數(shù)對![]() 稱為孿生素數(shù).在不超過20的素數(shù)中,隨機(jī)選取兩個不同的數(shù),其中能夠組成孿生素數(shù)的概率是( )
稱為孿生素數(shù).在不超過20的素數(shù)中,隨機(jī)選取兩個不同的數(shù),其中能夠組成孿生素數(shù)的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】王老師在做折紙游戲,現(xiàn)有一張邊長為1的正三角形紙片ABC,將點A翻折后恰好落在邊BC上的點F處,折痕為DE,設(shè)![]() ,
,![]() .
.
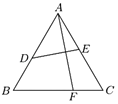
(1)求x、y滿足的關(guān)系式;
(2)求x的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,求
時,求![]() 的最小值;
的最小值;
(2)若函數(shù)![]() 在
在![]() 上存在極值點,求實數(shù)
上存在極值點,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系![]() 中,點
中,點![]() 分別是橢圓
分別是橢圓![]() 的上、下頂點,線段
的上、下頂點,線段![]() 長為
長為![]() ,橢圓的離心率為
,橢圓的離心率為![]() .
.
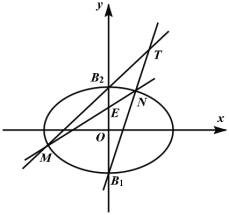
(1)求該橢圓的方程;
(2)已知過點![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 兩點,直線
兩點,直線![]() 與直線
與直線![]() 交于點
交于點![]() .
.
①若直線![]() 的斜率為
的斜率為![]() ,求點
,求點![]() 的坐標(biāo);
的坐標(biāo);
②求證點![]() 在一條定直線上,并寫出該直線方程.
在一條定直線上,并寫出該直線方程.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com