
【題目】已知函數(shù)![]() .
.
(1) 當![]() 時,解關于
時,解關于![]() 的不等式
的不等式![]() ;
;
(2) 若對任意![]() 及
及![]() 時,恒有
時,恒有![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1) ![]() (2)
(2) ![]()
【解析】試題分析:(Ⅰ)因為![]() ,所以不等式等價于
,所以不等式等價于![]() ,先利用導數(shù)研究函數(shù)
,先利用導數(shù)研究函數(shù)![]() 單調性:在
單調性:在![]() 上是增函數(shù),所以
上是增函數(shù),所以![]() (Ⅱ)不等式恒成立問題,一般轉化為對應函數(shù)最值問題,而對雙變量問題,先確定一變量,本題先看作
(Ⅱ)不等式恒成立問題,一般轉化為對應函數(shù)最值問題,而對雙變量問題,先確定一變量,本題先看作![]() 不等式恒成立問題,等價于
不等式恒成立問題,等價于![]() ,而利用導數(shù)易得
,而利用導數(shù)易得![]() 在
在![]() 上是減函數(shù),所以
上是減函數(shù),所以![]() ,即
,即![]() ,最后根據(jù)
,最后根據(jù)![]() 恒成立得
恒成立得![]() 因此
因此![]()
試題解析:解:(1)![]() ,
,
當![]() 時,恒有
時,恒有![]() ,則
,則![]() 在
在![]() 上是增函數(shù),
上是增函數(shù),
又![]() ,∴
,∴![]() 化為
化為![]() ,∴
,∴![]() .………………4分
.………………4分
(2)由題意知對任意![]() 及
及![]() 時,
時,
恒有![]() 成立,等價于
成立,等價于![]() ,
,
當![]() 時,由
時,由![]() 得
得![]() ,
,
因為![]() ,所以
,所以![]() ,
,
從而![]() 在
在![]() 上是減函數(shù),
上是減函數(shù),
所以![]() ,所以
,所以![]() ,即
,即![]() ,
,
因為![]() ,所以
,所以![]() ,所以實數(shù)
,所以實數(shù)![]() 的取值范圍為
的取值范圍為![]() .………………12分
.………………12分


 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知a∈R,設命題p:指數(shù)函數(shù)y=ax(a>0且a≠1)在R上單調遞增;命題q:函數(shù)y=ln(ax2﹣ax+1)的定義域為R,若“p且q”為假,“p或q”為真,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() 為
為![]() 上的偶函數(shù),當
上的偶函數(shù),當![]() 時,
時, ![]() .
.
(1)當![]() 時,求
時,求![]() 的解析式;
的解析式;
(2)當![]() 時,試比較
時,試比較![]() 與
與![]() 的大小;
的大小;
(3)求最小的整數(shù)![]() ,使得存在實數(shù)
,使得存在實數(shù)![]() ,對任意的
,對任意的![]() ,都有
,都有![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面是正方形,側面PAD⊥底面ABCD,且PA=PD= ![]() AD,若E、F分別為PC、BD的中點.
AD,若E、F分別為PC、BD的中點.
(Ⅰ) 求證:EF∥平面PAD;
(Ⅱ) 求證:EF⊥平面PDC.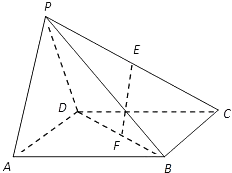
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知2件次品和3件正品混放在一起,現(xiàn)需要通過檢測將其區(qū)分,每次隨機檢測一件產品,檢測后不放回,直到檢測出2件次品或者檢測出3件正品時檢測結束.
(Ⅰ)求第一次檢測出的是次品且第二次檢測出的是正品的概率;
(Ⅱ)已知每檢測一件產品需要費用100元,設![]() 表示直到檢測出2件次品或者檢測出3件正品時所需要的檢測費用(單位:元),求
表示直到檢測出2件次品或者檢測出3件正品時所需要的檢測費用(單位:元),求![]() 的分布列和數(shù)學期望.
的分布列和數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在△ABC中,內角A,B,C所對的邊分別為a,b,c,已知A= ![]() ,b2﹣a2=
,b2﹣a2= ![]() c2 .
c2 .
(1)求tanC的值;
(2)若△ABC的面積為3,求b的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】給出下列五個命題: ①函數(shù) ![]() 的一條對稱軸是x=
的一條對稱軸是x= ![]() ;
;
②函數(shù)y=tanx的圖象關于點( ![]() ,0)對稱;
,0)對稱;
③正弦函數(shù)在第一象限為增函數(shù);
④若 ![]() ,則x1﹣x2=kπ,其中k∈Z;
,則x1﹣x2=kπ,其中k∈Z;
⑤函數(shù)f(x)=sinx+2|sinx|,x∈[0,2π]的圖象與直線y=k有且僅有兩個不同的交點,則k的取值范圍為(1,3).
以上五個命題中正確的有(填寫所有正確命題的序號)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,四棱錐P—ABCD中,PD![]() 底面ABCD,AB//DC,AD
底面ABCD,AB//DC,AD![]() DC,AB=AD=1,DC=2,PD=
DC,AB=AD=1,DC=2,PD=![]() ,M為棱PB的中點.
,M為棱PB的中點.
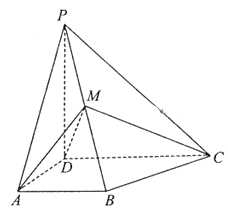
(1)證明:DM![]() 平面PBC;
平面PBC;
(2)求二面角A—DM—C的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列函數(shù)中,奇函數(shù)的個數(shù)為( ) ①y=x2sinx ②y=sinx , x∈ ![]() ③y=xcosx , x∈
③y=xcosx , x∈ ![]() ④y=tanx .
④y=tanx .
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com