
(1)建立適當的直角坐標系,求點M的軌跡方程;
(2)若曲線C是由點M的軌跡及其關于邊AB對稱的曲線組成的,F是AB邊上的一點,![]() =4,過點F的直線交曲線C于P、Q兩點,且
=4,過點F的直線交曲線C于P、Q兩點,且![]() ,求實數A的取值范圍.
,求實數A的取值范圍.
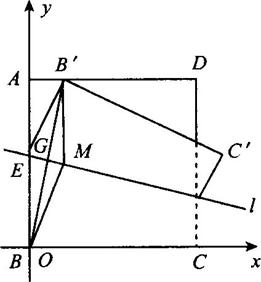
第19題圖
答案:以B為原點,BA所在直線為Y軸,BC所在直線為x軸,建立直角坐標系如圖.
(1)解法一:設B′(t,2),E(0,m),
其中0≤t≤2,0<m≤2.
∵![]() ,且
,且![]() ,
,
∴四邊形BEB′M是菱形,G(![]() t,1),M(f,2-m).
t,1),M(f,2-m).
且![]() ,即
,即![]() =0,
=0,
∵![]() =(t,2-2m),
=(t,2-2m),
∴![]() =(t,2),
=(t,2),
∴-t2=4m-4,即m=![]() t2+1.
t2+1.
設點M的坐標為(x,y),則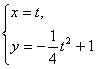 .
.
消去參數t,得y=![]() x2+1(0≤x≤2).
x2+1(0≤x≤2).
解法二:當B′不在A點處時.

第19題圖
∵![]() ,
,
∴四邊形BEB′M為平行四邊形.
依題意BE=EB′,
∴平行四邊形B′EBM為菱形,連接B′B交于l于G,則l是BB′的中垂線.
即M∈l,且B′M∥EB,
設B′(t,2),0≤t≤2,則G(![]() ,1)
,1)
∴l的方程為y-1=![]() .
.
設M(x,y),∵B′M∥EB,∴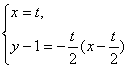
消去參數t,得x2=-4(y-1)(0<x≤2).
當B′在A點處時,![]() =0,
=0,
∴M、E重合于AB的中點,
∴M的坐標為(0,1),
∵M(0,1)也符合x2=-4(y-1).
∴M點的軌跡方程為x2=-4(y-1)(0≤x≤2).
(2)依題意知曲線C的方程為:
x2=-4(y-1)(-2≤x≤2).
設直線PQ的方程為:y=kx+![]() (
(![]() ≤k≤
≤k≤![]() ).
).
代入曲線C的方程并整理,得x2+4kx-2=0.
設P(x1,y1),Q(x2,y2),
則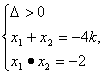 (*)
(*)
又∵![]() ,
,
∴(-x1,![]() -y1)=λ(x2,y2
-y1)=λ(x2,y2![]() ),
),
從而得x1=-λx2.
代人(*)得
①式兩邊平方后除以②式,得
![]() ,即
,即![]() =8k2
=8k2
∵0≤k2≤![]() .∴
.∴![]() .
.
即2λ2-5λ+2≤0,∴![]() ≤λ≤2.
≤λ≤2.
∴實數λ的取值范圍為[![]() ,2].
,2].


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
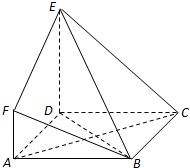 如圖,ABCD是邊長為3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE與平面ABCD所成角為60°.
如圖,ABCD是邊長為3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE與平面ABCD所成角為60°.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,ABCD是邊長為a的菱形,且∠BAD=60°,△PAD為正三角形,且面PAD⊥面ABCD.
如圖,ABCD是邊長為a的菱形,且∠BAD=60°,△PAD為正三角形,且面PAD⊥面ABCD.| AB |
| PD |
| EF |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,ABCD是邊長為2的正方形,面EAD⊥面ABCD,且EA=ED,EF∥AB,且EF=1,O是線段AD的中點,三棱錐F-OBC的體積為
如圖,ABCD是邊長為2的正方形,面EAD⊥面ABCD,且EA=ED,EF∥AB,且EF=1,O是線段AD的中點,三棱錐F-OBC的體積為| 2 | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2012•寧城縣模擬)如圖,ABCD是邊長為1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF.
(2012•寧城縣模擬)如圖,ABCD是邊長為1的正方形,DE⊥平面ABCD,AF∥DE,DE=2AF.查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,ABCD是邊長為2的正方形紙片,沿某動直線l為折痕將正方形在其下方的部分向上翻折,使得每次翻折后點B都落在邊AD上,記為B';折痕與AB交于點E,以EB和EB’為鄰邊作平行四邊形EB’MB.若以B為原點,BC所在直線為x軸建立直角坐標系(如下圖):
如圖,ABCD是邊長為2的正方形紙片,沿某動直線l為折痕將正方形在其下方的部分向上翻折,使得每次翻折后點B都落在邊AD上,記為B';折痕與AB交于點E,以EB和EB’為鄰邊作平行四邊形EB’MB.若以B為原點,BC所在直線為x軸建立直角坐標系(如下圖):查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com