
【題目】有一名高二學生盼望2020年進入某名牌大學學習,假設該名牌大學有以下條件之一均可錄取:①2020年2月通過考試進入國家數學奧賽集訓隊(集訓隊從2019年10月省數學競賽一等獎中選拔):②2020年3月自主招生考試通過并且達到2020年6月高考重點分數線,③2020年6月高考達到該校錄取分數線(該校錄取分數線高于重點線),該學生具備參加省數學競賽、自主招生和高考的資格且估計自己通過各種考試的概率如下表
省數學競賽一等獎 | 自主招生通過 | 高考達重點線 | 高考達該校分數線 |
0.5 | 0.6 | 0.9 | 0.7 |
若該學生數學競賽獲省一等獎,則該學生估計進入國家集訓隊的概率是0.2.若進入國家集訓隊,則提前錄取,若未被錄取,則再按②、③順序依次錄取:前面已經被錄取后,不得參加后面的考試或錄取.(注:自主招生考試通過且高考達重點線才能錄取)
(Ⅰ)求該學生參加自主招生考試的概率;
(Ⅱ)求該學生參加考試的次數![]() 的分布列及數學期望;
的分布列及數學期望;
(Ⅲ)求該學生被該校錄取的概率.
【答案】(Ⅰ)0.9.(Ⅱ)分布列見解析;數學期望3.3;(Ⅲ)0.838
【解析】
(Ⅰ)設該生參加省數學競賽獲一等獎、參加國家集訓隊時間分別為![]() ,
,![]() 則
則![]() ,然后利用互斥事件的概率公式進行求解;
,然后利用互斥事件的概率公式進行求解;
(Ⅱ)![]() 的可能取值為2,3,4,然后分別求出相應的概率,列出分布列,根據數學期望公式進行求解即可;
的可能取值為2,3,4,然后分別求出相應的概率,列出分布列,根據數學期望公式進行求解即可;
(Ⅲ)設自主招生通過并且高考達重點線錄取、自主招生未通過且高考達該校線錄取的事件分別為C、D,該學生被該校錄取的事件分為三種事件,AB、C、D,分別求出對應的概率,最后相加即可.
解:(Ⅰ)設該學生參加省數學競賽獲一等獎、參加國家集訓隊的事件分別為![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,![]()
![]() .
.
即該學生參加自主招生考試的概率為0.9.
(Ⅱ)該該學生參加考試的次數![]() 的可能取值為2,3,4
的可能取值為2,3,4
![]() ;
;
![]() ;
;
![]() .
.
所以![]() 的分布列為
的分布列為
| 2 | 3 | 4 |
| 0.1 | 0.5 | 0.4 |
![]() .
.
(Ⅲ)設該學生自主招生通過并且高考達到重點分數線錄取,自主招生未通過但高考達到該校錄取分數線錄取的事件分別為![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,
,
所以該學生被該校錄取的概率為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 右焦點為
右焦點為![]() ,右頂點為
,右頂點為![]() ,點
,點![]() 在橢圓上,且
在橢圓上,且![]() 軸,直線
軸,直線![]() 交
交![]() 軸于點
軸于點![]() ,若
,若![]() ;
;
(1)求橢圓的離心率;
(2)設經過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與橢圓在
與橢圓在![]() 軸上方的交點為
軸上方的交點為![]() ,圓
,圓![]() 同時與
同時與![]() 軸和直線
軸和直線![]() 相切,圓心
相切,圓心![]() 在直線
在直線![]() 上,且
上,且![]() . 求橢圓的方程.
. 求橢圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 與原點
與原點![]() 為圓心的圓相交所得弦長為
為圓心的圓相交所得弦長為![]() .
.
(1)若直線![]() 與圓
與圓![]() 切于第一象限,且直線
切于第一象限,且直線![]() 與坐標軸交于點
與坐標軸交于點![]() ,當
,當![]() 面積最小時,求直線
面積最小時,求直線![]() 的方程;
的方程;
(2)設![]() 是圓
是圓![]() 上任意兩點,點
上任意兩點,點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,若直線
,若直線![]() 分別交于
分別交于![]() 軸與點
軸與點![]() 和
和![]() ,問
,問![]() 是否為定值?若是,請求處該定值;若不是,請說明理由.
是否為定值?若是,請求處該定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() (a>b>0)的左焦點為F,上頂點為B. 已知橢圓的離心率為
(a>b>0)的左焦點為F,上頂點為B. 已知橢圓的離心率為![]() ,點A的坐標為
,點A的坐標為![]() ,且
,且![]() .
.
(I)求橢圓的方程;
(II)設直線l: ![]() 與橢圓在第一象限的交點為P,且l與直線AB交于點Q. 若
與橢圓在第一象限的交點為P,且l與直線AB交于點Q. 若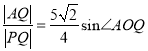 (O為原點) ,求k的值.
(O為原點) ,求k的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近日,某地普降暴雨,當地一大型提壩發生了滲水現象,當發現時已有![]() 的壩面滲水,經測算,壩而每平方米發生滲水現象的直接經濟損失約為
的壩面滲水,經測算,壩而每平方米發生滲水現象的直接經濟損失約為![]() 元,且滲水面積以每天
元,且滲水面積以每天![]() 的速度擴散.當地有關部門在發現的同時立即組織人員搶修滲水壩面,假定每位搶修人員平均每天可搶修滲水面積
的速度擴散.當地有關部門在發現的同時立即組織人員搶修滲水壩面,假定每位搶修人員平均每天可搶修滲水面積![]() ,該部門需支出服裝補貼費為每人
,該部門需支出服裝補貼費為每人![]() 元,勞務費及耗材費為每人每天
元,勞務費及耗材費為每人每天![]() 元.若安排
元.若安排![]() 名人員參與搶修,需要
名人員參與搶修,需要![]() 天完成搶修工作.
天完成搶修工作.
![]() 寫出
寫出![]() 關于
關于![]() 的函數關系式;
的函數關系式;
![]() 應安排多少名人員參與搶修,才能使總損失最小.(總損失=因滲水造成的直接損失+部門的各項支出費用)
應安排多少名人員參與搶修,才能使總損失最小.(總損失=因滲水造成的直接損失+部門的各項支出費用)
查看答案和解析>>
科目:高中數學 來源: 題型:
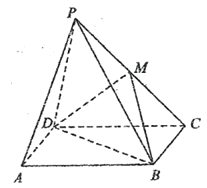
【題目】如圖,在四棱錐P—ABCD中,四邊形ABCD是矩形,平面PCD⊥平面ABCD,M為PC中點.求證:
(1)PA∥平面MDB;
(2)PD⊥BC.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com