Question

【題目】設數列的前項和為，點均在函數的圖象上.

(1)求證：數列為等差數列；

(2)設是數列的前項和，求使對所有都成立的最小正整數.

Answer 1

【答案】(1)詳見解析(2)10

【解析】

試題分析：(1)由題意得到關系式，由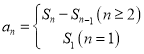可求得數列通項公式，從而證明數列為等差數列；(2) 首先整理的通項公式＝，依據特點采用裂項相消法求和可求得，從而得到最小正整數

試題解析：(1)依題意，＝3n－2，即Sn＝3n2－2n，…………………1分

n≥2時，an＝Sn－Sn－1＝(3n2－2n)－[3(n－1)2－2(n－1)]

＝6n－5. ……………………………………………3分

當n＝1時，a1＝S1＝1符合上式，…………………………4分

所以an＝6n－5(n∈N＋).…………………………5分

又∵an－an－1＝6n－5－[6(n－1)－5]＝6，

∴{an}是一個以1為首項，6為公差的等差數列.…………………………6分

(2)由(1)知，

＝＝…………………………8分

故Tn＝ [(1－)＋(－)＋…＋(－)]＝ (1－)，………10分

因此使得 (1－)< (n∈N＋)成立的m必須且僅需滿足≤，

即m≥10，故滿足要求的最小正整數m為10.…………………………12分