
【題目】如圖所示,四棱錐![]() 的底面
的底面![]() 是邊長為1的菱形,
是邊長為1的菱形,![]() ,
,
E是CD的中點,PA![]() 底面ABCD,
底面ABCD,![]() .
.
(I)證明:平面PBE![]() 平面PAB;
平面PAB;
(II)求二面角A—BE—P和的大小.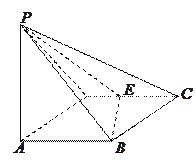
【答案】(I)同解析(II)二面角![]() 的大小為
的大小為![]()
【解析】
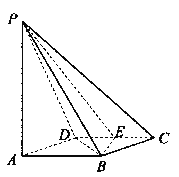
解:解法一(I)如圖所示, 連結![]() 由
由![]() 是菱形且
是菱形且![]() 知,
知,
![]() 是等邊三角形. 因為E是CD的中點,所以
是等邊三角形. 因為E是CD的中點,所以
![]() 又
又![]() 所以
所以![]()
又因為PA![]() 平面ABCD,
平面ABCD,![]() 平面ABCD,
平面ABCD,
所以![]() 而
而![]() 因此
因此![]() 平面PAB.
平面PAB.
又![]() 平面PBE,所以平面PBE
平面PBE,所以平面PBE![]() 平面PAB.
平面PAB.
(II)由(I)知,![]() 平面PAB,
平面PAB,![]() 平面PAB, 所以
平面PAB, 所以![]()
又![]() 所以
所以![]() 是二面角
是二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() .
.
故二面角![]() 的大小為
的大小為![]()
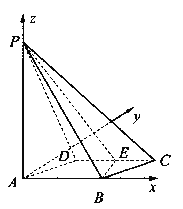
解法二:如圖所示,以A為原點,建立空間直角坐標系.則相關各點的坐標分別是
![]()
![]()
![]()
![]()
![]()
![]()
(I)因為![]() 平面PAB的一個法向量是
平面PAB的一個法向量是![]() 所以
所以![]() 和
和![]() 共線.
共線.
從而![]() 平面PAB. 又因為
平面PAB. 又因為![]() 平面PBE,所以平面PBE
平面PBE,所以平面PBE![]() 平面PAB.
平面PAB.
(II)易知![]() 設
設![]()
![]() 是平面PBE的一個法向量,
是平面PBE的一個法向量,
則由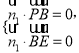 得
得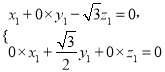 所以
所以![]()
故可取![]()
![]() 而平面ABE的一個法向量是
而平面ABE的一個法向量是![]()
于是,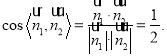 .
.
故二面角![]() 的大小為
的大小為![]()


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】越野汽車輪胎的質量是根據其正常使用的時間來衡量,使用時間越長,表明質量越好,且使用時間大于或等于6千小時的為優質品.現用![]() ,
,![]() 兩種不同型號的汽車輪胎做試驗,各隨機抽取部分產品作為樣本,得到試驗結果的頻率分布直方圖如圖所示,以上述試驗結果中各組的頻率作為相應的概率.
兩種不同型號的汽車輪胎做試驗,各隨機抽取部分產品作為樣本,得到試驗結果的頻率分布直方圖如圖所示,以上述試驗結果中各組的頻率作為相應的概率.

(1)現從大量的![]() ,
,![]() 兩種型號的輪胎中各隨機抽取2件產品,求其中至少有3件是優質品的概率;
兩種型號的輪胎中各隨機抽取2件產品,求其中至少有3件是優質品的概率;
(2)通過多年統計發現,![]() 型輪胎每件產品的利潤
型輪胎每件產品的利潤![]() (單位:元)與其使用時間
(單位:元)與其使用時間![]() (單位:千小時)的關系如下表:
(單位:千小時)的關系如下表:
使用時間 |
|
|
|
每件產品的利潤 |
| 200 | 400 |
若從大量的![]() 型輪胎中隨機抽取兩件,其利潤之和記為
型輪胎中隨機抽取兩件,其利潤之和記為![]() (單位:元),求
(單位:元),求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知邊長為![]() 米的正方形鋼板有一個角被銹蝕,其中
米的正方形鋼板有一個角被銹蝕,其中![]() 米,
米, ![]() 米.為了合理利用這塊鋼板,將在五邊形
米.為了合理利用這塊鋼板,將在五邊形![]() 內截取一個矩形塊
內截取一個矩形塊![]() ,使點
,使點![]() 在邊
在邊![]() 上.
上.
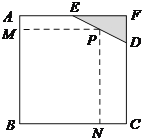
(1)設![]() 米,
米, ![]() 米,將
米,將![]() 表示成
表示成![]() 的函數,求該函數的解析式及定義域;
的函數,求該函數的解析式及定義域;
(2)求矩形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為 (t為參數).以
(t為參數).以![]() 為極點,x軸的非負半軸為極軸建立極坐標系,曲線
為極點,x軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值
的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(1)若![]() ,則
,則![]() ,
,![]() 滿足什么條件時,曲線
滿足什么條件時,曲線![]() 與
與![]() 在
在![]() 處總有相同的切線?
處總有相同的切線?
(2)當![]() 時,求函數
時,求函數![]() 的單調減區間;
的單調減區間;
(3)當![]() 時,若
時,若![]() 對任意的
對任意的![]() 恒成立,求
恒成立,求![]() 的取值的集合.
的取值的集合.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的個數是( )
①某同學投籃的命中率為0.6,他10次投籃中命中的次數![]() 是一個隨機變量,且
是一個隨機變量,且![]() ;
;
②某福彩中獎概率為![]() ,某人一次買了8張,中獎張數
,某人一次買了8張,中獎張數![]() 是一個隨機變量,且
是一個隨機變量,且![]() ;
;
③從裝有5個紅球、5個白球的袋中,有放回地摸球,直到摸出白球為止,則摸球次數![]() 是隨機變量,且
是隨機變量,且![]()
A.0個B.1個C.2個D.3個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com