
【題目】在棱長為2的正方體ABCD﹣A1B1C1D1中,E是BC的中點,F是DD1的中點, 
(1)求證:CF∥平面A1DE;
(2)求二面角A1﹣DE﹣A的余弦值.
【答案】
(1)解:分別以DA,DC,DD1為x軸,y軸,z軸建立空間直角坐標系,
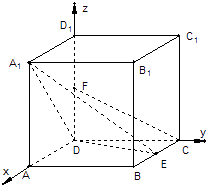
則A(2,0,0),A1(2,0,2),E(1,2,0),
D(0,0,0),C(0,2,0),F(0,0,1),則 ![]() =(2,0,2),
=(2,0,2), ![]() =(1,2,0).
=(1,2,0).
設平面A1DE的法向量是 ![]() ,
,
由 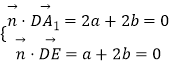 ,取
,取 ![]() =(﹣2,1,2).
=(﹣2,1,2).
由 ![]() =(0,﹣2,1),得
=(0,﹣2,1),得 ![]() ,所以CF∥平面A1DE.
,所以CF∥平面A1DE.
(2)面DEA的一個法向量為 ![]() .
.
cos< ![]() ,
, ![]() >=
>= ![]() .
.
∴面角A1﹣DE﹣A的余弦值為 ![]() .
.
【解析】先分別以DA,DC,DD1為x軸,y軸,z軸建立空間直角坐標系,則A(2,0,0),A1(2,0,2),E(1,2,0),D(0,0,0),C(0,2,0),F(0,0,1),再寫出向量 ![]() ,
, ![]() ,的坐標,求出平面A1DE的法向量
,的坐標,求出平面A1DE的法向量 ![]() .(1)利用向量坐標之間的關系證得
.(1)利用向量坐標之間的關系證得 ![]() ,從而得出CF∥平面A1DE.(2)利用法向量,利用向量的夾角公式求二面角A1﹣DE﹣A的余弦值.
,從而得出CF∥平面A1DE.(2)利用法向量,利用向量的夾角公式求二面角A1﹣DE﹣A的余弦值.
【考點精析】掌握直線與平面平行的判定是解答本題的根本,需要知道平面外一條直線與此平面內的一條直線平行,則該直線與此平面平行;簡記為:線線平行,則線面平行.


科目:高中數學 來源: 題型:
【題目】某算法的程序框圖如圖所示,其中輸入的變量![]() 在1,2,3,…,24這24個整數中等可能隨機產生.
在1,2,3,…,24這24個整數中等可能隨機產生.
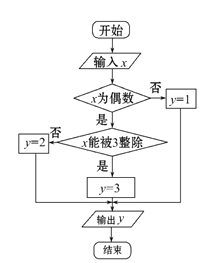
(Ⅰ)分別求出按程序框圖正確編程運行時輸出![]() 的值為
的值為![]() 的概率
的概率![]() (
(![]() =1,2,3);
=1,2,3);
(Ⅱ)甲、乙兩同學依據自己對程序框圖的理解,各自編寫程序重復運行n次后,統計記錄了輸出![]() 的值為
的值為![]() (
(![]() =1,2,3)的頻數.以下是甲、乙所作頻數統計表的部分數據.
=1,2,3)的頻數.以下是甲、乙所作頻數統計表的部分數據.
甲的頻數統計表(部分)
運行 次數n | 輸出y的值 為1的頻數 | 輸出y的值 為2的頻數 | 輸出y的值 為3的頻數 |
30 | 14 | 6 | 10 |
… | … | … | … |
2 100 | 1 027 | 376 | 697 |
乙的頻數統計表(部分)
運行 次數n | 輸出y的值 為1的頻數 | 輸出y的值 為2的頻數 | 輸出y的值 為3的頻數 |
30 | 12 | 11 | 7 |
… | … | … | … |
2 100 | 1 051 | 696 | 353 |
當n=2100時,根據表中的數據,分別寫出甲、乙所編程序各自輸出![]() 的值為
的值為![]() (
(![]() =1,2,3)的頻率(用分數表示),并判斷兩位同學中哪一位所編寫程序符合算法要求的可能性較大.
=1,2,3)的頻率(用分數表示),并判斷兩位同學中哪一位所編寫程序符合算法要求的可能性較大.
(Ⅲ)將按程序框圖正確編寫的程序運行3次,求輸出![]() 的值為2的次數ξ的分布列及數學期望.
的值為2的次數ξ的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點,離心率為
的左、右焦點,離心率為![]() ,
,![]() 分別是橢圓的上、下頂點,
分別是橢圓的上、下頂點,![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過![]() 作直線與
作直線與![]() 交于
交于![]() 兩點,求三角形
兩點,求三角形![]() 面積的最大值(
面積的最大值(![]() 是坐標原點).
是坐標原點).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4—4:坐標系與參數方程】
將圓![]() 上每一點的橫坐標保持不變,縱坐標變為原來的2倍,得曲線C.
上每一點的橫坐標保持不變,縱坐標變為原來的2倍,得曲線C.
(Ⅰ)寫出C的參數方程;
(Ⅱ)設直線![]() 與C的交點為
與C的交點為![]() ,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,求過線段
,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,求過線段![]() 的中點且與
的中點且與![]() 垂直的直線的極坐標方程.
垂直的直線的極坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校設計了一個實驗考察方案:考生從6道備選題中隨機抽取3道題,按照題目要求獨立完成全部實驗操作,規定:至少正確完成其中的2道題便可通過.己知6道備選題中考生甲有4道能正確完成,2道題不能完成;考生乙每題正確完成的概率都是 ![]() ,且每題正確完成與否互不影響.
,且每題正確完成與否互不影響.
(I) 求甲考生通過的概率;
(II) 求甲、乙兩考生正確完成題數的概率分布列,和甲、乙兩考生的數學期望;
(Ⅲ)請分析比較甲、乙兩考生的實驗操作能力.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在無窮數列![]() 中,
中,![]() ,對于任意
,對于任意![]() ,都有
,都有![]() ,
,![]() . 設
. 設![]() , 記使得
, 記使得![]() 成立的
成立的![]() 的最大值為
的最大值為![]() .
.
(1)設數列![]() 為1,3,5,7,
為1,3,5,7,![]() ,寫出
,寫出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)若![]() 為等差數列,求出所有可能的數列
為等差數列,求出所有可能的數列![]() ;
;
(3)設![]() ,
,![]() ,求
,求![]() 的值.(用
的值.(用![]() 表示)
表示)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com