
【題目】某同學(xué)用“五點(diǎn)法”畫函數(shù)f(x)=Asin(ωx+φ)(ω>0,|φ|![]() )在某一個周期內(nèi)的圖象時,列表并填入了部分?jǐn)?shù)據(jù),如表:
)在某一個周期內(nèi)的圖象時,列表并填入了部分?jǐn)?shù)據(jù),如表:
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ) | 0 | 5 | ﹣5 | 0 |
(1)請將上表數(shù)據(jù)補(bǔ)充完整,并直接寫出函數(shù)f(x)的解析式;
(2)將y=f(x)圖象上所有點(diǎn)向左平移θ(θ>0)個單位長度,得到y=g(x)的圖象.若y=g(x)圖象的一個對稱中心為(![]() ,0),求θ的最小值.
,0),求θ的最小值.
(3)若![]() ,求
,求![]() 的值.
的值.

| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)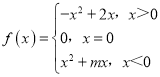 是奇函數(shù),則實(shí)數(shù)m的值是______;若函數(shù)f(x)在區(qū)間[-1,a-2]上滿足對任意x1≠x2,都有
是奇函數(shù),則實(shí)數(shù)m的值是______;若函數(shù)f(x)在區(qū)間[-1,a-2]上滿足對任意x1≠x2,都有![]() 成立,則實(shí)數(shù)a的取值范圍是______.
成立,則實(shí)數(shù)a的取值范圍是______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校高三年級50名學(xué)生參加數(shù)學(xué)競賽,根據(jù)他們的成績繪制了如圖所示的頻率分布直方圖,已知分?jǐn)?shù)在![]() 的矩形面積為
的矩形面積為![]() ,
,

求:![]() 分?jǐn)?shù)在
分?jǐn)?shù)在![]() 的學(xué)生人數(shù);
的學(xué)生人數(shù);
![]() 這50名學(xué)生成績的中位數(shù)
這50名學(xué)生成績的中位數(shù)![]() 精確到
精確到![]() ;
;
![]() 若分?jǐn)?shù)高于60分就能進(jìn)入復(fù)賽,從不能進(jìn)入復(fù)賽的學(xué)生中隨機(jī)抽取兩名,求兩人來自不同組的概率.
若分?jǐn)?shù)高于60分就能進(jìn)入復(fù)賽,從不能進(jìn)入復(fù)賽的學(xué)生中隨機(jī)抽取兩名,求兩人來自不同組的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知四棱錐![]() 的底面為菱形,且
的底面為菱形,且![]() ,
, ![]() 是
是![]() 中點(diǎn).
中點(diǎn).

(Ⅰ)證明: ![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,
, ![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】國內(nèi)某知名大學(xué)有男生14000人,女生10000人.該校體育學(xué)院想了解本校學(xué)生的運(yùn)動狀況,根據(jù)性別采取分層抽樣的方法從全校學(xué)生中抽取120人,統(tǒng)計他們平均每天運(yùn)動的時間(已知該校學(xué)生平均每天運(yùn)動的時間范圍是![]()
![]() ),如下表所示.
),如下表所示.
男生平均每天運(yùn)動的時間分布情況:

女生平均每天運(yùn)動的時間分布情況:
![]()
(1)假設(shè)同組中的每個數(shù)據(jù)均可用該組區(qū)間的中間值代替,請根據(jù)樣本估算該校男生平均每天運(yùn)動的時間(結(jié)果精確到0.1).
(2)若規(guī)定平均每天運(yùn)動的時間不少于![]() 的學(xué)生為“運(yùn)動達(dá)人”,低于
的學(xué)生為“運(yùn)動達(dá)人”,低于![]() 的學(xué)生為“非運(yùn)動達(dá)人”.
的學(xué)生為“非運(yùn)動達(dá)人”.
(ⅰ)根據(jù)樣本估算該校“運(yùn)動達(dá)人”的數(shù)量;
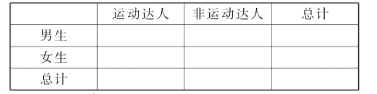
(ⅱ)請根據(jù)上述表格中的統(tǒng)計數(shù)據(jù)填寫下面![]() 列聯(lián)表,并通過計算判斷能否在犯錯誤的概率不超過0.05的前提下認(rèn)為“運(yùn)動達(dá)人”與性別有關(guān).
列聯(lián)表,并通過計算判斷能否在犯錯誤的概率不超過0.05的前提下認(rèn)為“運(yùn)動達(dá)人”與性別有關(guān).
參考公式:  ,其中
,其中![]() .
.
參考數(shù)據(jù):
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知等差數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,數(shù)列
,數(shù)列![]() 是等比數(shù)列,且滿足
是等比數(shù)列,且滿足![]() ,
, ![]() ,
, ![]() .
.
(1)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,若
,若![]() 對一切正整數(shù)
對一切正整數(shù)![]() 都成立,求
都成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
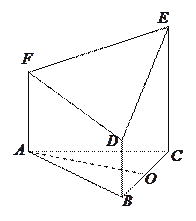
【題目】如圖所示的幾何體是由以等邊三角形![]() 為底面的棱柱被平面
為底面的棱柱被平面![]() 所截而得,已知
所截而得,已知![]() 平面
平面![]()
![]()
![]()
![]() 為
為![]() 的中點(diǎn),
的中點(diǎn), ![]() 面
面![]() .
.
(1)求![]() 的長;
的長;
(2)求證:面![]() 面
面![]() ;
;
(3)求平面![]() 與平面
與平面![]() 相交所成銳角二面角的余弦值.
相交所成銳角二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】己知橢圓W:![]() +
+![]() =1(a>b>0),直線
=1(a>b>0),直線![]() :
:![]() =
=![]() 與
與![]() 軸,
軸,![]() 軸的交點(diǎn)分別是橢圓W的焦點(diǎn)與頂點(diǎn)。
軸的交點(diǎn)分別是橢圓W的焦點(diǎn)與頂點(diǎn)。

(1)求橢圓W的方程;
(2)設(shè)直線m:![]() =kx(k≠0)與橢圓W交于P,Q兩點(diǎn),過點(diǎn)P(
=kx(k≠0)與橢圓W交于P,Q兩點(diǎn),過點(diǎn)P(![]() ,
,![]() )作PC⊥軸,垂足為點(diǎn)C,直線
)作PC⊥軸,垂足為點(diǎn)C,直線![]() 交橢圓w于另一點(diǎn)R。
交橢圓w于另一點(diǎn)R。
①求△PCQ面積的最大值;②求出∠QPR的大小。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(題文)已知等差數(shù)列{an}的首項(xiàng)a1≠0,前n項(xiàng)和為Sn,且S4+a2=2S3;等比數(shù)列{bn}滿足b1=a2,b2=a4.
(1)求證:數(shù)列{bn}中的每一項(xiàng)都是數(shù)列{an}中的項(xiàng);
(2)若a1=2,設(shè)cn=![]() ,求數(shù)列{cn}的前n項(xiàng)和Tn;
,求數(shù)列{cn}的前n項(xiàng)和Tn;
(3)在(2)的條件下,若有f(n)=log3Tn,求f(1)+f(2)+…+f(n)的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com