
【題目】如圖是根據某行業網站統計的某一年1月到12月(共12個月)的山地自行車銷售量(![]() 代表1000輛)折線圖,其中橫軸代表月份,縱軸代表銷售量,由折線圖提供的數據回答下列問題:
代表1000輛)折線圖,其中橫軸代表月份,縱軸代表銷售量,由折線圖提供的數據回答下列問題:
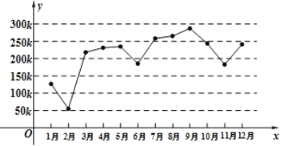
(1)在一年中隨機取一個月的銷售量,估計銷售量不足![]() 的概率;
的概率;
(2)在一年中隨機取連續兩個月的銷售量,估計這連續兩個月銷售量遞增(如2月到3月遞增)的概率;
(3)根據折線圖,估計年平均銷售量在哪兩條相鄰水平平行線線之間(只寫出結果,不要過程)
【答案】(1)![]() (2)
(2)![]() (3)在
(3)在![]() 這兩條水平線之間
這兩條水平線之間
【解析】
(1)設銷售量不足![]() 為事件
為事件![]() ,這一年共有12個月,利用列舉法能求出銷售量不足
,這一年共有12個月,利用列舉法能求出銷售量不足![]() 的概率.
的概率.
(2)設連續兩個月銷售量遞增為事件![]() ,利用列舉法能求出這連續兩個月銷售量遞增(如2月到3月遞增)的概率.
,利用列舉法能求出這連續兩個月銷售量遞增(如2月到3月遞增)的概率.
(3)由折線圖,估計年平均銷售量在![]() 這兩條水平線之間.
這兩條水平線之間.
解:(1)設銷售量不足![]() 為事件
為事件![]() ,
,
這一年共有12個月,
其中1月,2月,6月,11月共4個的銷售量不足![]() ,
,
所以![]() .
.
(2)設連續兩個月銷售量遞增為事件![]() ,
,
在這一年中隨機取連續兩個月的銷售量,
有1,2月;2,3月;3,4月;4,5月;5,6月;6,7月;7,8月;8,9月;9,10月;10,11月;11,12月共11種取法,
其中2,3月,3,4月;4,5月;6,7月;7,8月;8,9月;
11,12月共7種情況的銷售量遞增,
所以![]() .
.
(3)由折線圖,年平均銷售量在![]() 這兩條水平線之間.
這兩條水平線之間.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】過雙曲線![]() 的左焦點
的左焦點![]() 作圓
作圓![]() 的切線交雙曲線的右支于點
的切線交雙曲線的右支于點![]() ,且切點為
,且切點為![]() ,已知
,已知![]() 為坐標原點,
為坐標原點,![]() 為線段
為線段![]() 的中點(
的中點(![]() 點在切點
點在切點![]() 的右側),若
的右側),若![]() 的周長為
的周長為![]() ,則雙曲線的漸近線的方程為( )
,則雙曲線的漸近線的方程為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A,B是拋物線C:y2=4x上兩點,線段AB的垂直平分線與x軸有唯一的交點P(x0,0).
(1)求證:x0>2;
(2)若直線AB過拋物線C的焦點F,且|AB|=10,求|PF|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年10月份鄭州市進行了高三學生的體育學業水平測試,為了考察高中學生的身體素質比情況,現抽取了某校1000名(男生800名,女生200名)學生的測試成績,根據性別按分層抽樣的方法抽取100名進行分析,得到如下統計圖表:
男生測試情況:
抽樣情況 | 病殘免試 | 不合格 | 合格 | 良好 | 優秀 |
人數 | 5 | 10 | 15 | 47 |
|
女生測試情況
抽樣情況 | 病殘免試 | 不合格 | 合格 | 良好 | 優秀 |
人數 | 2 | 3 | 10 |
| 2 |
(1)現從抽取的1000名且測試等級為“優秀”的學生中隨機選出兩名學生,求選出的這兩名學生恰好是一男一女的概率;
(2)若測試等級為“良好”或“優秀”的學生為“體育達人”,其它等級的學生(含病殘免試)為“非體育達人”,根據以上統計數據填寫下面列聯表,并回答能否在犯錯誤的概率不超過0.010的前提下認為“是否為體育達人”與性別有關?
男性 | 女性 | 總計 | |
體育達人 | |||
非體育達人 | |||
總計 |
臨界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附:(  ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】去年年底,某商業集團公司根據相關評分細則,對其所屬25家商業連鎖店進行了考核評估.將各連鎖店的評估分數按[60,70), [70,80), [80,90), [90,100),分成四組,其頻率分布直方圖如下圖所示,集團公司依據評估得分,將這些連鎖店劃分為A,B,C,D四個等級,等級評定標準如下表所示.
評估得分 | [60,70) | [70,80) | [80,90) | [90,100) |
評定等級 | D | C | B | A |

(1)估計該商業集團各連鎖店評估得分的眾數和平均數;
(2)從評估分數不小于80分的連鎖店中任選2家介紹營銷經驗,求至少選一家A等級的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年1月31日晚上月全食的過程分為初虧、食既、食甚、生光、復圓五個階段,月食的初虧發生在19時48分,20時51分食既,21時29分食甚,22時07分生光,23時11分復圓.月全食伴隨有藍月亮和紅月亮,全食階段的“紅月亮”在食既時刻開始,生光時刻結束.小明準備在19:55至21:56之間的某個時刻欣賞月全食,則他等待“紅月亮”的時間不超過30分鐘的概率是________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年在印度尼西亞日惹舉辦的亞洲乒乓球錦標賽男子團體決賽中,中國隊與韓國隊相遇,中國隊男子選手A,B,C,D,E依次出場比賽,在以往對戰韓國選手的比賽中他們五人獲勝的概率分別是0.8,0.8,0.8,0.75,0.7,并且比賽勝負相互獨立.賽會釆用5局3勝制,先贏3局者獲得勝利.
(1)在決賽中,中國隊以3∶1獲勝的概率是多少?
(2)求比賽局數的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一塊半圓形的空地,直徑![]() 米,政府計劃在空地上建一個形狀為等腰梯形的花圃
米,政府計劃在空地上建一個形狀為等腰梯形的花圃![]() ,如圖所示,其中
,如圖所示,其中![]() 為圓心,
為圓心,![]() ,
,![]() 在半圓上,其余為綠化部分,設
在半圓上,其余為綠化部分,設![]() .
.
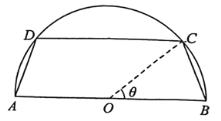
(1)記花圃的面積為![]() ,求
,求![]() 的最大值;
的最大值;
(2)若花圃的造價為10元/米,在花圃的邊![]() 、
、![]() 處鋪設具有美化效果的灌溉管道,鋪設費用為500元/米,兩腰
處鋪設具有美化效果的灌溉管道,鋪設費用為500元/米,兩腰![]() 、
、![]() 不鋪設,求
不鋪設,求![]() 滿足什么條件時,會使總造價最大.
滿足什么條件時,會使總造價最大.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com