
【題目】
如圖所示多面體中,AD⊥平面PDC,ABCD為平行四邊形,E,F分別為AD,BP的中點(diǎn),AD=![]() ,AP=
,AP=![]() ,PC=
,PC=![]() .
.
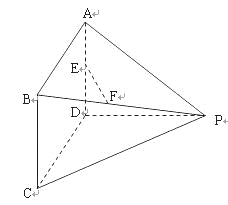
(Ⅰ)求證:EF∥平面PDC;
(Ⅱ)若∠CDP=90°,求證BE⊥DP;
(Ⅲ)若∠CDP=120°,求該多面體的體積.
【答案】(1)、(2)見(jiàn)解析;(3)![]() .
.
【解析】
(Ⅰ)取PC的中點(diǎn)為O,連FO,DO,
∵F,O分別為BP,PC的中點(diǎn),
∴![]() ∥BC,且
∥BC,且![]() ,
,
又ABCD為平行四邊形,![]() ∥BC,且
∥BC,且![]() ,
,
∴![]() ∥ED,且
∥ED,且![]()
∴四邊形EFOD是平行四邊形
即EF∥DO又EF![]() 平面PDC
平面PDC
∴EF∥平面PDC.
(Ⅱ)若∠CDP=90°,則PD⊥DC,
又AD⊥平面PDC∴AD⊥DP,
∴PD⊥平面ABCD,
∵BE![]() 平面ABCD,
平面ABCD,
∴BE⊥DP
(Ⅲ)連結(jié)AC,由ABCD為平行四邊形可知![]() 與
與![]() 面積相等,
面積相等,
所以三棱錐![]() 與三棱錐
與三棱錐![]() 體積相等,
體積相等,
即五面體的體積為三棱錐![]() 體積的二倍.
體積的二倍.
∵AD⊥平面PDC,∴AD⊥DP,由AD=3,AP=5,可得DP=4
又∠CDP=120°PC=2![]() ,
,
由余弦定理并整理得![]() , 解得DC=2
, 解得DC=2
∴![]() 三棱錐
三棱錐![]() 的體積
的體積![]()
∴該五面體的體積為![]()



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三棱柱![]() 中,每個(gè)側(cè)面均為正方形,D為底邊AB的中點(diǎn),E為側(cè)棱
中,每個(gè)側(cè)面均為正方形,D為底邊AB的中點(diǎn),E為側(cè)棱![]() 的中點(diǎn).
的中點(diǎn).

(1)求證:![]() 平面
平面![]() ;
;
(2)求證:![]() 平面
平面![]() ;
;
(3)若![]() ,求三棱錐
,求三棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某市為了了解民眾對(duì)開(kāi)展創(chuàng)建文明城市工作以來(lái)的滿意度,隨機(jī)調(diào)查了40名群眾,并將他們隨機(jī)分成A,B兩組,每組20人,A組群眾給第一階段的創(chuàng)文工作評(píng)分,B組群眾給第二階段的創(chuàng)文工作評(píng)分,根據(jù)兩組群眾的評(píng)分繪制了如圖莖葉圖:

![]() 根據(jù)莖葉圖比較群眾對(duì)兩個(gè)階段創(chuàng)文工作滿意度評(píng)分的平均值及集中程度
根據(jù)莖葉圖比較群眾對(duì)兩個(gè)階段創(chuàng)文工作滿意度評(píng)分的平均值及集中程度![]() 不要求計(jì)算出具體值,給出結(jié)論即可
不要求計(jì)算出具體值,給出結(jié)論即可![]() ;
;
![]() 根據(jù)群眾的評(píng)分將滿意度從低到高分為三個(gè)等級(jí):
根據(jù)群眾的評(píng)分將滿意度從低到高分為三個(gè)等級(jí):
滿意度評(píng)分 | 低于70分 | 70分到89分 | 不低于90分 |
滿意度等級(jí) | 不滿意 | 滿意 | 非常滿意 |
![]() 由頻率估計(jì)概率,判斷該市開(kāi)展創(chuàng)文工作以來(lái)哪個(gè)階段的民眾滿意率高?說(shuō)明理由.
由頻率估計(jì)概率,判斷該市開(kāi)展創(chuàng)文工作以來(lái)哪個(gè)階段的民眾滿意率高?說(shuō)明理由.
![]() 完成下面的列聯(lián)表,并根據(jù)列聯(lián)表判斷是否有
完成下面的列聯(lián)表,并根據(jù)列聯(lián)表判斷是否有![]() 的把握認(rèn)為民眾對(duì)兩個(gè)階段創(chuàng)文工作的滿意度存在差異?
的把握認(rèn)為民眾對(duì)兩個(gè)階段創(chuàng)文工作的滿意度存在差異?
低于70分 | 不低于70分 | |
第一階段 | ||
第二階段 |
附:![]()
|
|
|
|
k |
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某人設(shè)計(jì)一項(xiàng)單人游戲,規(guī)則如下:先將一棋子放在如圖所示正方形![]() (邊長(zhǎng)為2個(gè)單位)的頂點(diǎn)
(邊長(zhǎng)為2個(gè)單位)的頂點(diǎn)![]() 處,然后通過(guò)擲骰子來(lái)確定棋子沿正方形的邊按逆時(shí)針?lè)较蛐凶叩膯挝唬绻麛S出的點(diǎn)數(shù)為
處,然后通過(guò)擲骰子來(lái)確定棋子沿正方形的邊按逆時(shí)針?lè)较蛐凶叩膯挝唬绻麛S出的點(diǎn)數(shù)為![]() ,則棋子就按逆時(shí)針?lè)较蛐凶?/span>
,則棋子就按逆時(shí)針?lè)较蛐凶?/span>![]() 個(gè)單位,一直循環(huán)下去.則某人拋擲三次骰子后棋子恰好又回到點(diǎn)
個(gè)單位,一直循環(huán)下去.則某人拋擲三次骰子后棋子恰好又回到點(diǎn)![]() 處的所有不同走法共有( )
處的所有不同走法共有( )

A. 22種 B. 24種 C. 25種 D. 27種
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知向量![]() ,
,![]() 是坐標(biāo)原點(diǎn),若
是坐標(biāo)原點(diǎn),若![]() ,且
,且![]() 方向是沿
方向是沿![]() 的方向繞著
的方向繞著![]() 點(diǎn)按逆時(shí)針?lè)较蛐D(zhuǎn)
點(diǎn)按逆時(shí)針?lè)较蛐D(zhuǎn)![]() 角得到的,則稱
角得到的,則稱![]() 經(jīng)過(guò)一次
經(jīng)過(guò)一次![]() 變換得到
變換得到![]() ,現(xiàn)有向量
,現(xiàn)有向量![]() 經(jīng)過(guò)一次
經(jīng)過(guò)一次![]() 變換后得到
變換后得到![]() ,
,![]() 經(jīng)過(guò)一次
經(jīng)過(guò)一次![]() 變換后得到
變換后得到![]() ,…,如此下去,
,…,如此下去,![]() 經(jīng)過(guò)一次
經(jīng)過(guò)一次![]() 變換后得到
變換后得到![]() ,設(shè)
,設(shè)![]() ,
,![]() ,
,![]() ,則
,則![]() 等于( )
等于( )
A.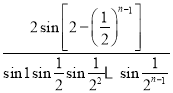 B.
B.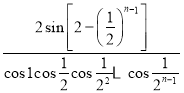
C.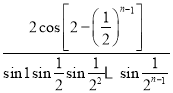 D.
D.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】(題文)
等邊△ABC的邊長(zhǎng)為3,點(diǎn)D,E分別為AB,AC上的點(diǎn),且滿足![]() (如圖①),將△ADE沿DE折起到△A1DE的位置,使二面角A1﹣DE﹣B成直二面角,連接A1B,A1C(如圖②).
(如圖①),將△ADE沿DE折起到△A1DE的位置,使二面角A1﹣DE﹣B成直二面角,連接A1B,A1C(如圖②).
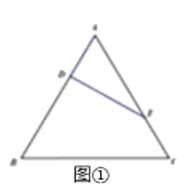
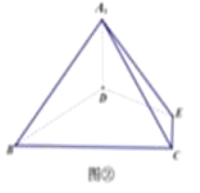
(1)求證:A1D⊥平面BCED;
(2)在線段BC上是否存在點(diǎn)P(不包括端點(diǎn)),使直線PA1與平面A1BD所成的角為60°?若存在,求出A1P的長(zhǎng),若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】故宮博物院五一期間同時(shí)舉辦“戲曲文化展”、“明代御窖瓷器展”、“歷代青綠山水畫(huà)展”、 “趙孟頫書(shū)畫(huà)展”四個(gè)展覽.某同學(xué)決定在五一當(dāng)天的上、下午各參觀其中的一個(gè),且至少參觀一個(gè)畫(huà)展,則不同的參觀方案共有
A. 6種 B. 8種 C. 10種 D. 12種
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() .
.
(Ⅰ)若![]() ,求函數(shù)
,求函數(shù)![]() 在
在![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)方程![]() 有3個(gè)不同的實(shí)根,求實(shí)數(shù)
有3個(gè)不同的實(shí)根,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅲ)當(dāng)![]() 時(shí),若對(duì)于任意的
時(shí),若對(duì)于任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,求滿足條件的正整數(shù)
,求滿足條件的正整數(shù)![]() 的取值的集合.
的取值的集合.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示的多面體中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,CM⊥AB,垂足為M,且AE=AC=2![]() ,BD=2BC=4,
,BD=2BC=4,
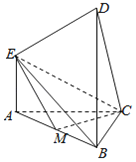
(1)求證:CM⊥ME;
(2)求二面角A﹣MC﹣E的余弦值.
(3)在線段DC上是否存在一點(diǎn)N,使得直線BN∥平面EMC,若存在,求出![]() 的值;若不存在,請(qǐng)說(shuō)明理由.
的值;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com