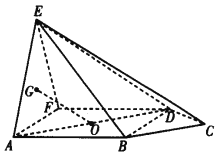
【題目】如圖所示，在五棱錐
中，側面
底面
，
是邊長為2的正三角形，四邊形
為正方形，
，且
，
是的重心，
是正方形的中心.
（Ⅰ）求證：
平面
；
（Ⅱ）求二面角
的余弦值.
【答案】（Ⅰ）見解析；（Ⅱ）
【解析】
（1）證明線面平行，轉化為線線平行．取
中點
，
中點
，連接
，
即可．（2）求二面角
的余弦值，以為原點，以
方向為
軸正方向，以
方向為
軸正方向，以
方向為
軸正方向，建立空間直角坐標系即可．
（Ⅰ）取中點，中點，連接，，易知
，，
，四點共線.
由
，且
，可知
為等腰直角三角形，所以
.
因為是正方形
的中心，所以
.
所以
，所以
.又
是
的重心，所以
.
所以
，故
.又因為
平面
，
平面.
所以
平面.
（Ⅱ）解法一：因為為中點，是正三角形，所以
.
因為側面
底面
，且交線為，所以
底面.所以直線
，
，
兩兩垂直.
如圖，以為原點，以方向為軸正方向，以方向為軸正方向，以方向為軸正方向，建立空間直角坐標系.
則
，
，
，
.所以
，
，
.
設平面
的法向量為
，
則
令
，則
.
設平面
的法向量為
，
則
，令
，則
.
所以
.
結合圖可知，二面角的余弦值為.
解法二：取
，
中點分別為
，
，連接
，
，則
.
又側面底面，
，側面
底面
，所以
平面
.
又
平面，所以
，所以
.
又
，
，所以
，所以
.
所以
為二面角的平面角.
易知
，所以
.因為
，
，
所以
，所以
.
即二面角的余弦值為.
科目：高中數學 來源： 題型：
【題目】如圖，三棱柱
的側面
是平行四邊形，
，平面
平面，且
分別是
的中點.
（Ⅰ）求證：
；
（Ⅱ）求證：
平面
；
（Ⅲ）在線段
上是否存在點
，使得
平面
？若存在，求出
的值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“科技引領，布局未來”科技研發是企業發展的驅動力量.2007年至2018年，某企業連續12年累計研發投入達4100億元，我們將研發投入與經營收入的比值記為研發投入占營收比．這12年間的研發投入（單位：十億元）用圖中的條形圖表示，研發投入占營收比用圖中的折線圖表示．
根據折線圖和條形圖，下列結論錯誤的是（ ）
A. 2012﹣2013 年研發投入占營收比增量相比 2017﹣2018 年增量大
B. 該企業連續 12 年研發投入逐年增加
C. 2015﹣2016 年研發投入增值最大
D. 該企業連續 12 年研發投入占營收比逐年增加
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，等腰梯形ABCD中，AB∥CD，AD=AB=BC=1，CD=2，E為CD中點，AE與BD交于點O，將△ADE沿AE折起，使點D到達點P的位置（P平面ABCE）．
（Ⅰ）證明：平面POB⊥平面ABCE；
（Ⅱ）若直線PB與平面ABCE所成的角為
，求二面角A-PE-C的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2013年華人數學家張益唐證明了孿生素數猜想的一個弱化形式。孿生素數猜想是希爾伯特在1900年提出的23個問題之一，可以這樣描述：存在無窮多個素數p，使得p+2是素數，素數對(p，p+2)稱為孿生素數．在不超過30的素數中，隨機選取兩個不同的數，其中能夠組成孿生素數的概率是
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知圓錐的頂點為S，底面圓O的兩條直徑分別為AB和CD，且AB⊥CD，若平面
平面
．現有以下四個結論：
①AD∥平面SBC；
②
；
③若E是底面圓周上的動點，則△SAE的最大面積等于△SAB的面積；
④
與平面SCD所成的角為45°．
其中正確結論的序號是__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示的幾何體，是將高為2、底面半徑為1的圓柱沿過旋轉軸的平面切開后，將其中一半沿切面向右水平平移后形成的封閉體.
分別為
的中點，
為弧
的中點，
為弧
的中點.
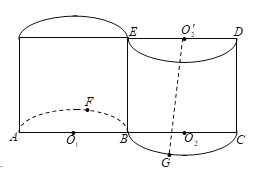
（1）求直線
與底面
所成的角的大小；
（2）求異面直線
與所成的角的大小（結果用反三角函數值表示）.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
