
【題目】在平面直角坐標系中,已知點A(2,0),B(0,2),C(cosα,sinα).
(1)若 ![]() ,且α∈(0,π),求角α的值;
,且α∈(0,π),求角α的值;
(2)若 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)解:由題意可得 ![]() =(cosα﹣2,sinα),
=(cosα﹣2,sinα), ![]() =(cosα,sinα﹣2),
=(cosα,sinα﹣2),
∵ ![]() ,∴(cosα﹣2)2+sin2α=cos2α+(sinα﹣2)2,且α∈(0,π).
,∴(cosα﹣2)2+sin2α=cos2α+(sinα﹣2)2,且α∈(0,π).
整理可得tanα=1,α= ![]()
(2)解:若 ![]() ,則 (cosα﹣2)cosα+sinα(sinα﹣2)=
,則 (cosα﹣2)cosα+sinα(sinα﹣2)= ![]() ,
,
化簡得 sinα+cosα= ![]() ,平方可得 1+2sinαcosα=
,平方可得 1+2sinαcosα= ![]() ,2sinαcosα=﹣
,2sinαcosα=﹣ ![]() ,
,
∴ ![]() =
= ![]() =2sinαcosα=﹣
=2sinαcosα=﹣ ![]() .
.
【解析】(1)求得 ![]() 和
和 ![]() 的坐標,再根據
的坐標,再根據 ![]() 以及α∈(0,π),求得tanα 的值可得α 的值.(2)由
以及α∈(0,π),求得tanα 的值可得α 的值.(2)由 ![]() ,求得 sinα+cosα=
,求得 sinα+cosα= ![]() ,平方可得2sinαcosα=﹣
,平方可得2sinαcosα=﹣ ![]() ,再根據
,再根據 ![]() =2sinαcosα,求得結果.
=2sinαcosα,求得結果.
【考點精析】解答此題的關鍵在于理解同角三角函數基本關系的運用的相關知識,掌握同角三角函數的基本關系:![]()
![]() ;
;![]()
![]() ;(3) 倒數關系:
;(3) 倒數關系:![]() .
.


 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:高中數學 來源: 題型:
【題目】在正三棱柱ABC﹣A1B1C1中,點D是BC的中點. 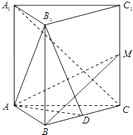
(1)求證:A1C∥平面AB1D;
(2)設M為棱CC1的點,且滿足BM⊥B1D,求證:平面AB1D⊥平面ABM.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法錯誤的是_____________.
①.如果命題“![]() ”與命題“
”與命題“![]() 或
或![]() ”都是真命題,那么命題
”都是真命題,那么命題![]() 一定是真命題.
一定是真命題.
②.命題![]() ,則
,則![]()
③.命題“若![]() ,則
,則![]() ”的否命題是:“若
”的否命題是:“若![]() ,則
,則![]() ”
”
④.特稱命題 “![]() ,使
,使![]() ”是真命題.
”是真命題.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=lnx﹣ax(a∈R).
(1)若直線y=3x﹣1是函數f(x)圖象的一條切線,求實數a的值;
(2)若函數f(x)在[1,e2]上的最大值為1﹣ae(e為自然對數的底數),求實數a的值;
(3)若關于x的方程ln(2x2﹣x﹣3t)+x2﹣x﹣t=ln(x﹣t)有且僅有唯一的實數根,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代的數學巨著,內容極為豐富,書中有如下問題:“今有五人分五錢,令上二人所得與下三人等,問各得幾何.”意思是:“5人分取5錢,各人所得錢數依次成等差數列,其中前2人所得錢數之和與后3人所得錢數之和相等.”,則其中分得錢數最多的是( )
A.![]() 錢
錢
B.1錢
C.![]() 錢
錢
D.![]() 錢
錢
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區2007年至2013年農村居民家庭純收入y(單位:千元)的數據如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代號t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均純收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y關于t的線性回歸方程;
(2)利用(1)中的回歸方程,分析2007年至2013年該地區農村居民家庭人均純收入的變化情況,并預測該地區2015年農村居民家庭人均純收入.
附:回歸直線的斜率和截距的最小二乘法估計公式分別為:
 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中曲線 ![]() 經伸縮變換
經伸縮變換 ![]() 后得到曲線C2 , 在以O為極點,x軸的正半軸為極軸的極坐標系中,曲線C3的極坐標方程為
后得到曲線C2 , 在以O為極點,x軸的正半軸為極軸的極坐標系中,曲線C3的極坐標方程為 ![]() .
.
(1)求曲線C2的參數方程和C3的直角坐標方程;
(2)設M為曲線C2上的一點,又M向曲線C3引切線,切點為N,求|MN|的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com