
【題目】已知定義在![]() 上的函數(shù)
上的函數(shù)![]() 滿足:
滿足:![]() 對任意的實數(shù)
對任意的實數(shù)![]() 都成立,當且僅當
都成立,當且僅當![]() 時取等號,則稱函數(shù)
時取等號,則稱函數(shù)![]() 是
是![]() 上的
上的![]() 函數(shù),已知
函數(shù),已知![]() 函數(shù)
函數(shù)![]() 具有性質(zhì):
具有性質(zhì):![]() (
(![]() ,
,![]() )對任意的實數(shù)
)對任意的實數(shù)![]() (
(![]() )都成立,當且僅當
)都成立,當且僅當![]() 時取等號.
時取等號.
(1)試判斷函數(shù)![]() (
(![]() 且
且![]() )是否是
)是否是![]() 上的
上的![]() 函數(shù),說明理由;
函數(shù),說明理由;
(2)求證:![]() 是
是![]() 上的
上的![]() 函數(shù),并求
函數(shù),并求![]() 的最大值(其中
的最大值(其中![]() 、
、![]() 、
、![]() 是△
是△![]() 三個內(nèi)角);
三個內(nèi)角);
(3)若![]() 定義域為
定義域為![]() ,
,
① ![]() 是奇函數(shù),證明:
是奇函數(shù),證明:![]() 不是
不是![]() 上的
上的![]() 函數(shù);
函數(shù);
② ![]() 最小正周期為
最小正周期為![]() ,證明:
,證明:![]() 不是
不是![]() 上的
上的![]() 函數(shù).
函數(shù).
【答案】(1)![]() ,是S函數(shù);
,是S函數(shù);![]() ,不是S函數(shù);(2)見解析,最大值
,不是S函數(shù);(2)見解析,最大值![]() ;(3)見解析.
;(3)見解析.
【解析】
(1)利用S函數(shù)的定義證明當0<a<1時,![]() 不是
不是![]() 上的
上的![]() 函數(shù). 當a大于1時,
函數(shù). 當a大于1時,![]() 不是
不是![]() 上的
上的![]() 函數(shù).(2)利用S函數(shù)的定義證明
函數(shù).(2)利用S函數(shù)的定義證明![]() 是
是![]() 上的
上的![]() 函數(shù),并利用S函數(shù)的性質(zhì)求
函數(shù),并利用S函數(shù)的性質(zhì)求![]() 的最大值.(3)利用舉反例證明.
的最大值.(3)利用舉反例證明.
任取![]() ,
,
當![]()
![]()
![]()
![]()
同理可證,當0<a<1時,![]() 不是
不是![]() 上的
上的![]() 函數(shù).
函數(shù).
(2)![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]()
![]()
![]()
所以![]() 是
是![]() 上的
上的![]() 函數(shù).
函數(shù).
由S函數(shù)的性質(zhì)有![]()
所以![]()
![]()
(3)用舉反例證明,
令f(x)=sinx,
所以f(x)=sinx是R上的周期為π的奇函數(shù),
取![]()
所以![]()
而![]()
![]()
即在R上,f(x)=sinx不是S函數(shù),故原命題得證.


 學練快車道快樂假期寒假作業(yè)系列答案
學練快車道快樂假期寒假作業(yè)系列答案科目:高中數(shù)學 來源: 題型:
【題目】某景點為了了解游客人數(shù)的變化規(guī)律,提高旅游服務(wù)質(zhì)量,收集并整理了2016年1月至2018年12月期間月接待游客量(單位:萬人)的數(shù)據(jù),繪制了下面的折線圖:

根據(jù)該折線圖,下列結(jié)論正確的是( )
A.各年1月至8月月接待游客量逐月增加
B.各年8月至12月月接待游客量逐月遞減
C.各年的月接待游客量最低峰期在12月
D.各年1月至6月的月接待游客量相對于7月至12月,波動性更小,變化比較平穩(wěn)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設(shè)曲線y=xn+1(n∈N*)在點(1,1)處的切線與x軸的交點的橫坐標為xn,令an=lgxn,則a1+a2+…+a99的值為( )
A. 1 B. 2 C. -2 D. -1
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】每年10月中上旬是小麥的最佳種植時間,但小麥的發(fā)芽會受到土壤、氣候等多方面因素的影響.某科技小組為了解晝夜溫差的大小與小麥發(fā)芽的多少之間的關(guān)系,在不同的溫差下統(tǒng)計了100顆小麥種子的發(fā)芽數(shù),得到了如下數(shù)據(jù):
溫差 | 8 | 10 | 11 | 12 | 13 |
發(fā)芽數(shù) | 79 | 81 | 85 | 86 | 90 |
(1)請根據(jù)統(tǒng)計的最后三組數(shù)據(jù),求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)若由(1)中的線性回歸方程得到的估計值與前兩組數(shù)據(jù)的實際值誤差均不超過兩顆,則認為線性回歸方程是可靠的,試判斷(1)中得到的線性回歸方程是否可靠;
(3)若100顆小麥種子的發(fā)芽率為![]() 顆,則記為
顆,則記為![]() 的發(fā)芽率,當發(fā)芽率為
的發(fā)芽率,當發(fā)芽率為![]() 時,平均每畝地的收益為
時,平均每畝地的收益為![]() 元,某農(nóng)場有土地10萬畝,小麥種植期間晝夜溫差大約為
元,某農(nóng)場有土地10萬畝,小麥種植期間晝夜溫差大約為![]() ,根據(jù)(1)中得到的線性回歸方程估計該農(nóng)場種植小麥所獲得的收益.
,根據(jù)(1)中得到的線性回歸方程估計該農(nóng)場種植小麥所獲得的收益.
附:在線性回歸方程![]() 中,
中,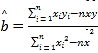 .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某校從![]() 名教師中選派
名教師中選派![]() 名教師去完成
名教師去完成![]() 項不同的工作,每人至少完成一項,每項工作由
項不同的工作,每人至少完成一項,每項工作由![]() 人完成,其中甲和乙不同去,甲和丙只能同去或同不去,則不同的選派方案種數(shù)是( )
人完成,其中甲和乙不同去,甲和丙只能同去或同不去,則不同的選派方案種數(shù)是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 過點
過點![]() 且離心率為
且離心率為![]() .
.
(1)求橢圓C的方程;
(2)是否存在過點![]() 的直線
的直線![]() 與橢圓C相交于A,B兩點,且滿足
與橢圓C相交于A,B兩點,且滿足![]() .若存在,求出直線
.若存在,求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】海水養(yǎng)殖場進行某水產(chǎn)品的新、舊網(wǎng)箱養(yǎng)殖方法的產(chǎn)量對比,收獲時各隨機抽取了100個網(wǎng)箱,測量各箱水產(chǎn)品的產(chǎn)量(單位:![]() )得頻率分布直方圖如下:
)得頻率分布直方圖如下:


(1)設(shè)兩種養(yǎng)殖方法的箱產(chǎn)量相互獨立,記![]() 表示事件:“舊養(yǎng)殖法的箱產(chǎn)量低于
表示事件:“舊養(yǎng)殖法的箱產(chǎn)量低于![]() ,新養(yǎng)殖法的箱產(chǎn)量不低于
,新養(yǎng)殖法的箱產(chǎn)量不低于![]() ”,估計
”,估計![]() 的概率;
的概率;
(2)填寫下面![]() 列聯(lián)表,并根據(jù)聯(lián)表判斷是否有
列聯(lián)表,并根據(jù)聯(lián)表判斷是否有![]() 的把握認為箱產(chǎn)量與養(yǎng)殖方法有關(guān):
的把握認為箱產(chǎn)量與養(yǎng)殖方法有關(guān):
箱產(chǎn)量 | 箱產(chǎn)量 | |
舊養(yǎng)殖法 | ||
新養(yǎng)殖法 |
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(3)根據(jù)箱產(chǎn)量的頻率分布直方圖,求新養(yǎng)殖法箱產(chǎn)量的中位數(shù)的估計值(精確到0.01)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標原點為極點,
為參數(shù)),以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求![]() 和
和![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)若曲線![]() 截直線
截直線![]() 所得線段的中點坐標為
所得線段的中點坐標為![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com