
【題目】設![]() 是實數,
是實數,![]() ,
,
(1)若函數![]() 為奇函數,求
為奇函數,求![]() 的值;
的值;
(2)試用定義證明:對于任意![]() ,
,![]() 在
在![]() 上為單調遞增函數;
上為單調遞增函數;
(3)若函數![]() 為奇函數,且不等式
為奇函數,且不等式![]() 對任意
對任意![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍。
的取值范圍。
【答案】(1)![]() (2)詳見解析(3)
(2)詳見解析(3)![]()
【解析】
試題分析:(1)函數f(x)為奇函數,故可得f(x)+f(-x)=0,由此方程求m的值;(2)證明于任意m,f(x)在R上為單調函數,由定義法證明即可,設![]() ∈R,
∈R,![]() ,研究
,研究![]() 的符號,根據單調性的定義判斷出結果;(3)因為f(x)在R上為增函數且為奇函數,由此可以將不等式
的符號,根據單調性的定義判斷出結果;(3)因為f(x)在R上為增函數且為奇函數,由此可以將不等式![]() 對任意x∈R恒成立,轉化為
對任意x∈R恒成立,轉化為![]() 即
即![]() 對任意x∈R恒成立,再通過換元進一步轉化為二次不等式恒成立的問題即可解出此時的恒成立的條件
對任意x∈R恒成立,再通過換元進一步轉化為二次不等式恒成立的問題即可解出此時的恒成立的條件
試題解析:(1)∵![]() ,且
,且![]()
∴![]() (注:通過
(注:通過![]() 求也同樣給分)∴
求也同樣給分)∴![]()
(2)證明:設![]() ,則
,則![]()
![]()
![]() ∵
∵![]() ∴
∴![]()
∴![]() 即
即![]() 。 所以
。 所以![]() 在R上為增函數。
在R上為增函數。
(3)因為![]() 為奇函數且在R上為增函數,
為奇函數且在R上為增函數,
由![]() 得:
得: ![]()
∴![]()
![]() 對任意
對任意![]() 恒成立。
恒成立。
令![]()
![]() 問題等價于
問題等價于![]() 對任意
對任意![]() 恒成立。
恒成立。
令![]() ,其對稱軸
,其對稱軸![]()
當![]() 即
即![]() 時,
時,![]() ,符合題意。
,符合題意。
當![]() 時,即
時,即![]() 時,對任意
時,對任意![]() ,
,![]() 恒成立,等價于
恒成立,等價于![]()
解得:![]()
綜上所述,當![]() 時,不等式
時,不等式![]() 對任意
對任意![]() 恒成立
恒成立


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知斜三棱柱![]() 的底面是直角三角形,
的底面是直角三角形,![]() ,側棱與底面所成角為
,側棱與底面所成角為![]() ,點
,點![]() 在底面上身影
在底面上身影![]() 落在
落在![]() 上.
上.

(1)求證:![]() 平面
平面![]() ;
;
(2)若點![]() 恰為
恰為![]() 中點,且
中點,且![]() ,求
,求![]() 的大小;
的大小;
(3)若![]() ,且當
,且當![]() 時,求二面角
時,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】性格色彩學創始人樂嘉是江蘇電視臺當紅節目“非誠勿擾”的特約嘉賓,他的點評視角獨特,語言犀利,給觀眾留下了深刻的印象,某報社為了了解觀眾對樂嘉的喜愛程度,隨機調查了觀看了該節目的140名觀眾,得到如下的列聯表:(單位:名)
男 | 女 | 總計 | ||||||
喜愛 | 40 | 60 | 100 | |||||
不喜愛 | 20 | 20 | 40 | |||||
總計 | 60 | 80 | 140 | |||||
p(k2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | |||
k0 | 2.705 | 3.841 | 5.024 | 6.635 | 7.879 | |||
(Ⅰ)從這60名男觀眾中按對樂嘉是否喜愛采取分層抽樣,抽取一個容量為6的樣本,問樣本中喜愛與不喜愛的觀眾各有多少名?
(Ⅱ)根據以上列聯表,問能否在犯錯誤的概率不超過0.025的前提下認為觀眾性別與喜愛樂嘉有關?(精確到0.001)
(Ⅲ)從(Ⅰ)中的6名男性觀眾中隨機選取兩名作跟蹤調查,求選到的兩名觀眾都喜愛樂嘉的概率.
附: 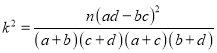
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知p:指數函數f(x)=(2a-6)x在R上是單調減函數;q:關于x的方程x2-3ax+2a2+1=0的兩根均大于3,若p或q為真,p且q為假,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 為自然對數的底數.
為自然對數的底數.
(Ⅰ)若![]() 和
和![]() 在區間
在區間![]() 內具有相同的單調性,求實數
內具有相同的單調性,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)若![]() ,且函數
,且函數![]() 的最小值為
的最小值為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義域為R的函數![]() 是奇函數
是奇函數
(1)求![]() 的值
的值
(2)判斷f(x)在![]() 上的單調性。(直接寫出答案,不用證明)
上的單調性。(直接寫出答案,不用證明)
(3)若對于任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在區間
在區間![]() 上為單調遞增函數,求
上為單調遞增函數,求![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,函數
時,函數![]() 的圖象與
的圖象與![]() 軸交于兩點
軸交于兩點![]() 且
且![]() ,又
,又![]() 是
是![]() 的導函數.若正常數
的導函數.若正常數![]() 滿足條件
滿足條件![]() .證明:
.證明: ![]() <0.
<0.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com