
【題目】在中國,不僅是購物,而且從共享單車到醫院掛號再到公共繳費,日常生活中幾乎全部領域都支持手機支付.出門不帶現金的人數正在迅速增加。中國人民大學和法國調查公司益普索合作,調查了騰訊服務的6000名用戶,從中隨機抽取了60名,統計他們出門隨身攜帶現金(單位:元)如莖葉圖如示,規定:隨身攜帶的現金在100元以下(不含100元)的為“手機支付族”,其他為“非手機支付族”.

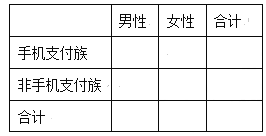
(1)根據上述樣本數據,將![]() 列聯表補充完整,并判斷有多大的把握認為“手機支付族”與“性別”有關?
列聯表補充完整,并判斷有多大的把握認為“手機支付族”與“性別”有關?
(2)用樣本估計總體,若從騰訊服務的用戶中隨機抽取3位女性用戶,這3位用戶中“手機支付族”的人數為![]() ,求隨機變量
,求隨機變量![]() 的期望和方差;
的期望和方差;
(3)某商場為了推廣手機支付,特推出兩種優惠方案,方案一:手機支付消費每滿1000元可直減100元;方案二:手機支付消費每滿1000元可抽獎2次,每次中獎的概率同為![]() ,且每次抽獎互不影響,中獎一次打9折,中獎兩次打8.5折.如果你打算用手機支付購買某樣價值1200元的商品,請從實際付款金額的數學期望的角度分析,選擇哪種優惠方案更劃算?
,且每次抽獎互不影響,中獎一次打9折,中獎兩次打8.5折.如果你打算用手機支付購買某樣價值1200元的商品,請從實際付款金額的數學期望的角度分析,選擇哪種優惠方案更劃算?
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
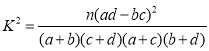
【答案】(1)列聯表見解析,99%;(2)![]() ,
,![]() ;(3)第二種優惠方案更劃算.
;(3)第二種優惠方案更劃算.
【解析】
(1)根據已知數據得出列聯表,再根據獨立性檢驗得出結論;
(2)有數據可知,女性中“手機支付族”的概率為![]() ,知
,知![]() 服從二項分布,即
服從二項分布,即![]() ,可求得其期望和方差;
,可求得其期望和方差;
(3)若選方案一,則需付款![]() 元,若選方案二,設實際付款
元,若選方案二,設實際付款![]() 元,,則
元,,則![]() 的取值為1200,1080,1020,求出實際付款的期望,再比較兩個方案中的付款的金額的大小,可得出選擇的方案.
的取值為1200,1080,1020,求出實際付款的期望,再比較兩個方案中的付款的金額的大小,可得出選擇的方案.
(1)由已知得出聯列表:
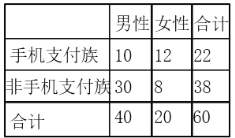 ,所以
,所以![]() ,
,
![]() 有99%的把握認為“手機支付族”與“性別”有關;
有99%的把握認為“手機支付族”與“性別”有關;
(2)有數據可知,女性中“手機支付族”的概率為![]() ,
,![]() ,
,
![]() ;
;
(3)若選方案一,則需付款![]() 元
元
若選方案二,設實際付款![]() 元,,則
元,,則![]() 的取值為1200,1080,1020,
的取值為1200,1080,1020,
![]() ,
,![]() ,
,![]() ,
,
![]()
![]() 選擇第二種優惠方案更劃算
選擇第二種優惠方案更劃算


科目:高中數學 來源: 題型:
【題目】設函數![]() .
.
(1)若![]() ,求函數
,求函數![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)若函數在![]() 和
和![]() 處有兩個極值點,其中
處有兩個極值點,其中![]() ,
,![]() .
.
(i)求實數![]() 的取值范圍;
的取值范圍;
(ii)若![]() (e為自然對數的底數),求
(e為自然對數的底數),求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)如圖,在多面體![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的的菱形,
的的菱形, ![]() ,四邊形
,四邊形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 和
和![]() 分別是
分別是![]() 和
和![]() 的中點.
的中點.
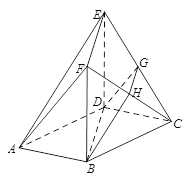
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 是定義在R上的偶函數,且當
是定義在R上的偶函數,且當![]() 時,
時,![]() (
(![]() ).
).
(1)當![]() 時,求
時,求![]() 的表達式:
的表達式:
(2)求![]() 在區間
在區間![]() 的最大值
的最大值![]() 的表達式;
的表達式;
(3)當![]() 時,若關于x的方程
時,若關于x的方程![]() (a,
(a,![]() )恰有10個不同實數解,求a的取值范圍.
)恰有10個不同實數解,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為橢圓
為橢圓![]()
![]() 的左、右焦點,離心率為
的左、右焦點,離心率為![]() ,點
,點![]() 在橢圓上.
在橢圓上.
(1)求橢圓![]() 的方程;
的方程;
(2)過![]() 的直線
的直線![]() 分別交橢圓于
分別交橢圓于![]() 和
和![]() ,且
,且![]() ,問是否存在常數
,問是否存在常數![]() ,使得
,使得![]() 成等差數列?若存在,求出
成等差數列?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知實數a滿足1<a≤2,設函數f (x)=![]() x3-
x3-![]() x2+ax.
x2+ax.
(Ⅰ) 當a=2時,求f (x)的極小值;
(Ⅱ) 若函數g(x)=4x3+3bx2-6(b+2)x (b∈R) 的極小值點與f (x)的極小值點相同,
求證:g(x)的極大值小于等于10.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com