Question

已知正方形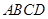的邊長為2，分別是邊的中點．
（1）在正方形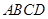內部隨機取一點，求滿足的概率；
（2）從這八個點中，隨機選取兩個點，記這兩個點之間的距離為，求隨機變量的分布列與數學期望．

Answer 1

（1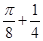）；（2）詳見解析

解析試題分析：（1）首先判斷這是一個幾何概型，然后找出符合條件的區域與總區域的面積，利用面積之比即可算出相應的古典概型的概率；（2）先確定這八個點連線距離的幾種情況，然后就不同的的值進行計算，利用離散型隨機變量的計算方法列表并計算相應的數學期望。
試題解析：（1）這是一個幾何概型．所有點構成的平面區域是正方形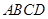的內部，其面積是．
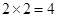1分
滿足的點構成的平面區域是以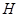為圓心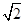，為半徑的圓的內部與正方形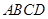內部的公共部分，它可以看作是由一個以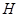為圓心、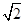為半徑、圓心角為的扇形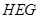的內部（即四分之一個圓）與兩個直角邊為1的等腰直角三角形（△和△）內部構成．                        2分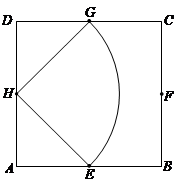

其面積是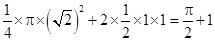．      3分
所以滿足的概率為．       4分
（2）從這八個點中，任意選取兩個點，共可構成條不同的線段．
5分
其中長度為1的線段有8條，長度為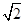的線段有4條，長度為2的線段有6條，長度為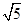的線段有8條，長度為的線段有2條．
所以所有可能的取值為．                    7分
且，        ，        ，
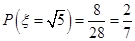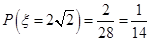，      ．                9分
所以隨機變量的分布列為：