
【題目】已知拋物線![]() 上一點(diǎn)
上一點(diǎn)![]() 到其準(zhǔn)線的距離為
到其準(zhǔn)線的距離為![]() .
.
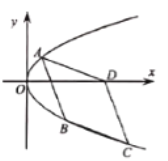
(1)求拋物線![]() 的方程;
的方程;
(2)如圖![]() 、
、![]() 、
、![]() 為拋物線
為拋物線![]() 上三個(gè)點(diǎn),
上三個(gè)點(diǎn),![]() ,若四邊形
,若四邊形![]() 為菱形,求四邊形
為菱形,求四邊形![]() 的面積.
的面積.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)利用拋物線的定義求出![]() 的值,進(jìn)而可得出拋物線
的值,進(jìn)而可得出拋物線![]() 的方程;
的方程;
(2)設(shè)點(diǎn)![]() 、
、![]() ,并設(shè)菱形
,并設(shè)菱形![]() 的中心為
的中心為![]() ,分
,分![]() 軸和
軸和![]() 與
與![]() 軸不垂直兩種情況討論,在
軸不垂直兩種情況討論,在![]() 軸時(shí),求出
軸時(shí),求出![]() 和
和![]() ,進(jìn)而可求得菱形
,進(jìn)而可求得菱形![]() 的面積,在
的面積,在![]() 與
與![]() 軸不垂直時(shí),設(shè)直線
軸不垂直時(shí),設(shè)直線![]() 方程
方程![]() ,可求得點(diǎn)
,可求得點(diǎn)![]() 的坐標(biāo),由此得出點(diǎn)
的坐標(biāo),由此得出點(diǎn)![]() 的坐標(biāo),結(jié)合已知條件求出
的坐標(biāo),結(jié)合已知條件求出![]() 和
和![]() 的值,進(jìn)而求得
的值,進(jìn)而求得![]() 和
和![]() ,由此得出菱形
,由此得出菱形![]() 的面積.
的面積.
(1)由已知可得![]() ,得
,得![]() ,拋物線
,拋物線![]() 的方程為
的方程為![]() ;
;
(2)設(shè)![]() 、
、![]() ,菱形
,菱形![]() 的中心
的中心![]() ,
,
當(dāng)![]() 軸,則
軸,則![]() 在原點(diǎn),
在原點(diǎn),![]() ,
,
此時(shí)![]() ,
,![]() ,菱形的面積
,菱形的面積![]() ;
;
當(dāng)![]() 與
與![]() 軸不垂直時(shí),設(shè)直線
軸不垂直時(shí),設(shè)直線![]() 方程
方程![]() ,則直線
,則直線![]() 的斜率為
的斜率為![]()
聯(lián)立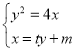 ,消去
,消去![]() 得
得![]() ,
,
所以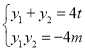 ,
,![]() ,
,
所以![]() ,
,![]() ,
,
![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() ,
,
![]() 點(diǎn)
點(diǎn)![]() 在拋物線上,且直線
在拋物線上,且直線![]() 的斜率為
的斜率為![]() .
.
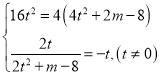 解得:
解得:![]() ,
,![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,
![]() .
.
綜上,![]() 或
或![]() .
.


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),
為參數(shù)),以坐標(biāo)原點(diǎn)為極點(diǎn),![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(Ⅰ)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)設(shè)![]() 為曲線
為曲線![]() 上的點(diǎn),
上的點(diǎn),![]() ,垂足為
,垂足為![]() ,若
,若![]() 的最小值為
的最小值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】2018年反映社會(huì)現(xiàn)實(shí)的電影《我不是藥神》引起了很大的轟動(dòng),治療特種病的創(chuàng)新藥研發(fā)成了當(dāng)務(wù)之急.為此,某藥企加大了研發(fā)投入,市場(chǎng)上治療一類(lèi)慢性病的特效藥品![]() 的研發(fā)費(fèi)用
的研發(fā)費(fèi)用![]() (百萬(wàn)元)和銷(xiāo)量
(百萬(wàn)元)和銷(xiāo)量![]() (萬(wàn)盒)的統(tǒng)計(jì)數(shù)據(jù)如下:
(萬(wàn)盒)的統(tǒng)計(jì)數(shù)據(jù)如下:
研發(fā)費(fèi)用 | 2 | 3 | 6 | 10 | 13 | 15 | 18 | 21 |
銷(xiāo)量 | 1 | 1 | 2 | 2.5 | 3.5 | 3.5 | 4.5 | 6 |
(1)根據(jù)數(shù)據(jù)用最小二乘法求出![]() 與
與![]() 的線性回歸方程
的線性回歸方程![]() (系數(shù)用分?jǐn)?shù)表示,不能用小數(shù));
(系數(shù)用分?jǐn)?shù)表示,不能用小數(shù));
(2)該藥企準(zhǔn)備生產(chǎn)藥品![]() 的三類(lèi)不同的劑型
的三類(lèi)不同的劑型![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 合格的概率分別為
合格的概率分別為![]() ,
,![]() ,
,![]() ,第二次檢測(cè)時(shí),三類(lèi)劑型
,第二次檢測(cè)時(shí),三類(lèi)劑型![]() ,
,![]() ,
,![]() 合格的概率分別為
合格的概率分別為![]() ,
,![]() ,
,![]() .兩次檢測(cè)過(guò)程相互獨(dú)立,設(shè)經(jīng)過(guò)兩次檢測(cè)后
.兩次檢測(cè)過(guò)程相互獨(dú)立,設(shè)經(jīng)過(guò)兩次檢測(cè)后![]() ,
,![]() ,
,![]() 三類(lèi)劑型合格的種類(lèi)數(shù)為
三類(lèi)劑型合格的種類(lèi)數(shù)為![]() ,求
,求![]() 的分布列與數(shù)學(xué)期望.
的分布列與數(shù)學(xué)期望.
附:(1)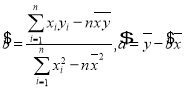 (2)
(2)![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() 的標(biāo)準(zhǔn)方程是
的標(biāo)準(zhǔn)方程是![]() ,設(shè)
,設(shè)![]() 是橢圓
是橢圓![]() 的左焦點(diǎn),
的左焦點(diǎn),![]() 為直線
為直線![]() 上任意一點(diǎn),過(guò)
上任意一點(diǎn),過(guò)![]() 做
做![]() 的垂線交橢圓
的垂線交橢圓![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() .
.
(1)證明:線段![]() 平分線段
平分線段![]() (其中
(其中![]() 為坐標(biāo)原點(diǎn));
為坐標(biāo)原點(diǎn));
(2)當(dāng)![]() 最小時(shí),求點(diǎn)
最小時(shí),求點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在正三棱柱![]() (側(cè)棱垂直于底面,且底面三角形
(側(cè)棱垂直于底面,且底面三角形![]() 是等邊三角形)中,
是等邊三角形)中,![]() ,
,![]() 分別是
分別是![]() 的中點(diǎn).
的中點(diǎn).
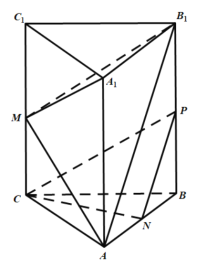
(1)求證:平面![]() ∥平面
∥平面![]() ;
;
(2)在線段![]() 上是否存在一點(diǎn)
上是否存在一點(diǎn)![]() 使
使![]() 平面
平面![]() ?若存在,確定點(diǎn)
?若存在,確定點(diǎn)![]() 的位置;若不存在,也請(qǐng)說(shuō)明理由.
的位置;若不存在,也請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】[選修4—4:坐標(biāo)系與參數(shù)方程]
以平面直角坐標(biāo)系的原點(diǎn)為極點(diǎn),x軸的正半軸為極軸,建立極坐標(biāo)系,兩種坐標(biāo)系中取相同的長(zhǎng)度單位.已知直線l的參數(shù)方程是![]() (t為參數(shù)),圓C的極坐標(biāo)方程是ρ=4cos θ,求直線l被圓C截得的弦長(zhǎng).
(t為參數(shù)),圓C的極坐標(biāo)方程是ρ=4cos θ,求直線l被圓C截得的弦長(zhǎng).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】橢圓![]() 的離心率是
的離心率是![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 做斜率為
做斜率為![]() 的直線
的直線![]() ,橢圓
,橢圓![]() 與直線
與直線![]() 交于
交于![]() 兩點(diǎn),當(dāng)直線
兩點(diǎn),當(dāng)直線![]() 垂直于
垂直于![]() 軸時(shí)
軸時(shí)![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)當(dāng)![]() 變化時(shí),在
變化時(shí),在![]() 軸上是否存在點(diǎn)
軸上是否存在點(diǎn)![]() ,使得
,使得![]() 是以
是以![]() 為底的等腰三角形,若存在求出
為底的等腰三角形,若存在求出![]() 的取值范圍,若不存在說(shuō)明理由.
的取值范圍,若不存在說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】2016年春節(jié)期間全國(guó)流行在微信群里發(fā)、搶紅包,現(xiàn)假設(shè)某人將688元發(fā)成手氣紅包50個(gè),產(chǎn)生的手氣紅包頻數(shù)分布表如表:

(I)求產(chǎn)生的手氣紅包的金額不小于9元的頻率;
(Ⅱ)估計(jì)手氣紅包金額的平均數(shù)(同一組中的數(shù)據(jù)用該組區(qū)間的中點(diǎn)值作代表);
(Ⅲ)在這50個(gè)紅包組成的樣本中,將頻率視為概率.
(i)若紅包金額在區(qū)間[21,25]內(nèi)為最佳運(yùn)氣手,求搶得紅包的某人恰好是最佳運(yùn)氣手的概率;
(ii)隨機(jī)抽取手氣紅包金額在[1,5)∪[﹣21,25]內(nèi)的兩名幸運(yùn)者,設(shè)其手氣金額分別為m,n,求事件“|m﹣n|>16”的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】明代商人程大位在公元1592年編撰完成《算法統(tǒng)宗》一書(shū).書(shū)中有如下問(wèn)題:“今有女子善織,初日遲,次日加倍,第三日轉(zhuǎn)速倍增,第四日又倍增,織成絹六丈七尺五寸.問(wèn)各日織若干?”意思是:“有一位女子善于織布,第一天由于不熟悉有點(diǎn)慢,第二天起每天織的布都是前一天的2倍,已知她前四天共織布6丈7尺5寸,問(wèn)這位女子每天織布多少?”根據(jù)文中的已知條件,可求得該女了第一天織布________尺,若織布一周(7天),共織________尺.(其中1丈為10尺,1尺為10寸)
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com