
【題目】如圖,在直四棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)當![]() 時,直線
時,直線![]() 與平面
與平面![]() 所成的角能否為
所成的角能否為![]() ?并說明理由.
?并說明理由.
【答案】(1)證明見解析;(2)答案見解析.
【解析】
(1)由題意結合幾何關系可證得![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)設![]() ,以
,以![]() 為原點,建立空間直角坐標系
為原點,建立空間直角坐標系![]() ,不妨設
,不妨設![]() ,
,![]() ,據此可得平面
,據此可得平面![]() 的法向量為
的法向量為![]() ,若滿足題意,則
,若滿足題意,則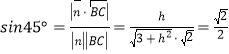 ,據此可得
,據此可得![]() ,矛盾,故直線
,矛盾,故直線![]() 與平面
與平面![]() 所成的角不可能為
所成的角不可能為![]() .
.
(1)證明:因為![]() ,
,![]() ,所以
,所以![]() 為正三角形,
為正三角形,
所以![]() ,又
,又![]() ,
,![]() 為公共邊,所以
為公共邊,所以![]() ,
,
所以![]() ,所以
,所以![]() .
.
又四棱柱![]() 為直棱柱,所以
為直棱柱,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)直線![]() 與平面
與平面![]() 所成的角不可能為
所成的角不可能為![]() .
.
設![]() ,以
,以![]() 為原點,建立空間直角坐標系
為原點,建立空間直角坐標系![]() 如圖所示,
如圖所示,
不妨設![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
則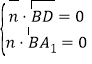 ,即
,即![]() ,
,
解得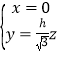 .
.
令![]() ,得
,得![]() ,
,
若直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,
,
則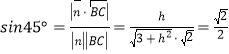 ,
,
整理得![]() ,矛盾,故直線
,矛盾,故直線![]() 與平面
與平面![]() 所成的角不可能為
所成的角不可能為![]() .
.


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案 新思維寒假作業系列答案
新思維寒假作業系列答案科目:高中數學 來源: 題型:
【題目】已知點A在直線2x-3y+5=0上移動,點P為連接M(4,-3)和點A的線段的中點,則點P的軌跡方程為
A. 2x-3y-6=0 B. 2x-3y+2=0 C. 2x-3y+11=0 D. 2x+3y-6=0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學用“五點法”畫函數![]() 在某一個周期內的圖象時,列表并填入了部分數據,如下表:
在某一個周期內的圖象時,列表并填入了部分數據,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)請將上表數據補充完整,填寫在相應位置,并求出函數![]() 的解析式;
的解析式;
(2)把![]() 的圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再把得到的圖象向左平移
的圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),再把得到的圖象向左平移![]() 個單位長度,得到函數
個單位長度,得到函數![]() 的圖象,求
的圖象,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現從某醫院中隨機抽取了七位醫護人員的關愛患者考核分數(患者考核:10分制),用相關的特征量![]() 表示;醫護專業知識考核分數(試卷考試:100分制),用相關的特征量
表示;醫護專業知識考核分數(試卷考試:100分制),用相關的特征量![]() 表示,數據如下表:
表示,數據如下表:
(Ⅰ)求![]() 關于
關于![]() 的線性回歸方程(計算結果精確到0.01);
的線性回歸方程(計算結果精確到0.01);
(Ⅱ)利用(I)中的線性回歸方程,分析醫護專業考核分數的變化對關愛患者考核分數的影響,并估計某醫護人員的醫護專業知識考核分數為95分時,他的關愛患者考核分數(精確到0.1);

(Ⅲ)現要從醫護專業知識考核分數95分以下的醫護人員中選派2人參加組建的“九寨溝災后醫護小分隊”培訓,求這兩人中至少有一人考核分數在90分以下的概率.
附:回歸方程![]() 中斜率和截距的最小二乘法估計公式分別為
中斜率和截距的最小二乘法估計公式分別為
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年9月24日,阿貝爾獎和菲爾茲獎雙料得主、英國著名數學家阿蒂亞爵士宣布自己證明了黎曼猜想,這一事件引起了數學屆的震動。在1859年的時候,德國數學家黎曼向科學院提交了題目為《論小于某值的素數個數》的論文并提出了一個命題,也就是著名的黎曼猜想。在此之前,著名數學家歐拉也曾研究過這個問題,并得到小于數字![]() 的素數個數大約可以表示為
的素數個數大約可以表示為![]() 的結論。若根據歐拉得出的結論,估計1000以內的素數的個數為_________(素數即質數,
的結論。若根據歐拉得出的結論,估計1000以內的素數的個數為_________(素數即質數,![]() ,計算結果取整數)
,計算結果取整數)
A. 768 B. 144 C. 767 D. 145
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校學生社團組織活動豐富,學生會為了解同學對社團活動的滿意程度,隨機選取了100位同學進行問卷調查,并將問卷中的這100人根據其滿意度評分值(百分制)按照[40,50),[50,60),[60,70),…,[90,100]分成6組,制成如圖所示頻率分布直方圖.
(1)求圖中x的值;
(2)求這組數據的中位數;
(3)現從被調查的問卷滿意度評分值在[60,80)的學生中按分層抽樣的方法抽取5人進行座談了解,再從這5人中隨機抽取2人作主題發言,求抽取的2人恰在同一組的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)解不等式![]() ;
;
(2)若函數![]() 在區間
在區間![]() 上存在零點,求實數
上存在零點,求實數![]() 的取值范圍;
的取值范圍;
(3)若函數![]() ,其中
,其中![]() 為奇函數,
為奇函數, ![]() 為偶函數,若不等式
為偶函數,若不等式![]() 對任意
對任意![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上.
上.
(1)求橢圓![]() 的方程;
的方程;
(2)已知![]() 與
與![]() 為平面內的兩個定點,過
為平面內的兩個定點,過![]() 點的直線
點的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
, ![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com