
【題目】如圖所示,直四棱柱![]() 的側棱
的側棱![]() 長為
長為![]() ,底面
,底面![]() 是邊長
是邊長![]()
![]() 的矩形,
的矩形,![]() 為
為![]() 的中點,
的中點,
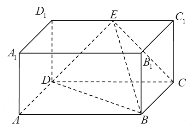
(1)求證:![]() 平面
平面![]() ,
,
(2)求異面直線![]() 與
與![]() 所成的角的大小(結果用反三角函數表示).
所成的角的大小(結果用反三角函數表示).
【答案】(1)見解析;(2)![]()
【解析】
(1)先證明EC⊥ED,再利用BC⊥平面CC1D1D,證明BC⊥DE,即可證明DE⊥平面EBC;
(2)取A1B1中點F,連接BF,DF,∠FBD即為所求異面直線的夾角(或其補角),確定△FBD為各邊長,根據余弦定理可求∠FBD余弦值,從而求異面直線BD與EC所成的角的大小.
(1)證明:∵直四棱柱![]() 的側棱
的側棱![]() 長為
長為![]() ,
,
底面ABCD是邊長AB=2a,BC=a的矩形,
![]() 為
為![]() 的中點,
的中點,
∴EC=ED=![]() a,CD=2a,
a,CD=2a,
∴EC⊥ED,
∵BC⊥平面![]() ,DE平面
,DE平面![]() ,
,
∴BC⊥DE,
∵BC∩EC=C
∴DE⊥平面EBC.
(2)取A1B1中點F,連接BF,DF,
易得EC∥FB,
∴∠FBD即為所求異面直線的夾角(或其補角),

連接D1F,△DD1F為直角三角形,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
![]()
根據余弦定理,![]() ,
,
∴![]() ,
,
∴異面直線![]() 與
與![]() 所成的角的大小為
所成的角的大小為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知定義在實數集![]() 上的偶函數
上的偶函數![]() 和奇函數
和奇函數![]() 滿足
滿足![]() .
.
(1)求![]() 與
與![]() 的解析式;
的解析式;
(2)求證:![]() 在區間
在區間![]() 上單調遞增;并求
上單調遞增;并求![]() 在區間
在區間![]() 的反函數;
的反函數;
(3)設![]() (其中
(其中![]() 為常數),若
為常數),若![]() 對于
對于![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,
中,![]() 平面ABCD,底面ABCD是正方形,
平面ABCD,底面ABCD是正方形,![]() ,E為PC上一點,當F為DC的中點時,EF平行于平面PAD.
,E為PC上一點,當F為DC的中點時,EF平行于平面PAD.
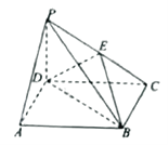
(Ⅰ)求證:![]() 平面PCB;
平面PCB;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】請你設計一個包裝盒,![]() 是邊長為
是邊長為![]() 的正方形硬紙片(如圖1所示),切去陰影部分所示的四個全等的等腰三角形,再沿虛線折起,使得
的正方形硬紙片(如圖1所示),切去陰影部分所示的四個全等的等腰三角形,再沿虛線折起,使得![]() ,
,![]() ,
,![]() ,
,![]() 四個點重合于圖2中的點
四個點重合于圖2中的點![]() ,正好形成一個正四棱錐形狀的包裝盒(如圖2所示),設正四棱錐
,正好形成一個正四棱錐形狀的包裝盒(如圖2所示),設正四棱錐![]() 的底面邊長為
的底面邊長為![]() .
.
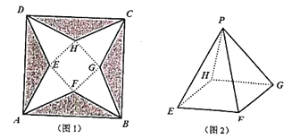
(1)若要求包裝盒側面積![]() 不小于
不小于![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(2)若要求包裝盒容積![]() 最大,試問
最大,試問![]() 應取何值?并求出此時包裝盒的容積.
應取何值?并求出此時包裝盒的容積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 數列
數列![]() 滿足
滿足![]() ;數列
;數列![]() 滿足
滿足![]() ;數列
;數列![]() 為公比大于1的等比數列,且
為公比大于1的等比數列,且![]() ,
,![]() 為方程
為方程![]() 的兩個不相等的實根.
的兩個不相等的實根.
(1)求數列![]() 和數列
和數列![]() 的通項公式;
的通項公式;
(2)將數列![]() 中的第
中的第![]() 項,第
項,第![]() 項,第
項,第![]() 項,……,第
項,……,第![]() 項,……刪去后剩余的項按從小到大的順序排成新數列
項,……刪去后剩余的項按從小到大的順序排成新數列![]() ,求數列
,求數列![]() 的前2013項和.
的前2013項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列![]() 的首項為
的首項為![]() ,公差為
,公差為![]() ,等比數列
,等比數列![]() 的首項為
的首項為![]() ,公比為
,公比為![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)求證:![]() ,并由
,并由![]() 推導
推導![]() 的值;
的值;
(2)若數列![]() 共有
共有![]() 項,前
項,前![]() 項的和為
項的和為![]() ,其后的
,其后的![]() 項的和為
項的和為![]() ,再其后的
,再其后的![]() 項的和為
項的和為![]() ,求
,求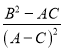 的比值.
的比值.
(3)若數列![]() 的前
的前![]() 項,前
項,前![]() 項、前
項、前![]() 項的和分別為
項的和分別為![]() ,試用含字母
,試用含字母![]() 的式子來表示
的式子來表示![]() (即
(即![]() ,且不含字母
,且不含字母![]() )
)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com