
【題目】某學校為了加強學生數學核心素養的培養,鍛煉學生自主探究學習的能力,他們以函數![]() 為基本素材,研究該函數的相關性質,取得部分研究成果如下:其中研究成果正確的是( )
為基本素材,研究該函數的相關性質,取得部分研究成果如下:其中研究成果正確的是( )
A.同學甲發現:函數的定義域為(﹣1,1),且f(x)是偶函數
B.同學乙發現:對于任意的x∈(﹣1,1),都有![]()
C.同學丙發現:對于任意的a,b∈(﹣1,1),都有![]()
D.同學丁發現:對于函數定義域內任意兩個不同的實數x1,x2,總滿足![]()
 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案科目:高中數學 來源: 題型:
【題目】如果f(x)是定義在R上的函數,且對任意的x∈R,均有f(-x)≠-f(x),則稱該函數是“X—函數”.
(1)分別判斷下列函數:①y=![]() ;②y=x+1;③y=x2+2x-3是否為“X—函數”?(直接寫出結論)
;②y=x+1;③y=x2+2x-3是否為“X—函數”?(直接寫出結論)
(2)若函數f(x)=x-x2+a是“X—函數”,求實數a的取值范圍;
(3)設“X—函數”f(x)=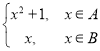 在R上單調遞增,求所有可能的集合A與B.
在R上單調遞增,求所有可能的集合A與B.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)滿足f(x+1)-f(x)=-2x+1,且f(2)=15.
(1)求函數f(x)的解析式;
(2) 令g(x)=(2-2m)x-f(x).
① 若函數g(x)在x∈[0,2]上是單調函數,求實數m的取值范圍;
② 求函數g(x)在x∈[0,2]上的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
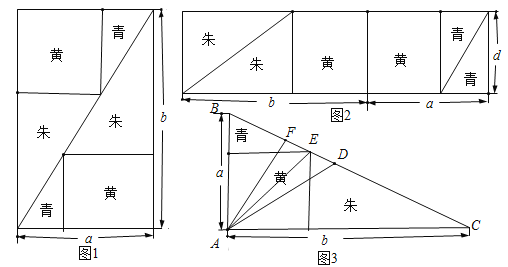
【題目】《九章算術》中“勾股容方”問題:“今有勾五步,股十二步,問勾中容方幾何?”魏晉時期數學家劉徽在其《九章算術注》中利用出入相補原理給出了這個問題的一般解法:如圖1,用對角線將長和寬分別為![]() 和
和![]() 的矩形分成兩個直角三角形,每個直角三角形再分成一個內接正方形(黃)和兩個小直角三角形(朱、青).將三種顏色的圖形進行重組,得到如圖2所示的矩形.該矩形長為
的矩形分成兩個直角三角形,每個直角三角形再分成一個內接正方形(黃)和兩個小直角三角形(朱、青).將三種顏色的圖形進行重組,得到如圖2所示的矩形.該矩形長為![]() ,寬為內接正方形的邊長
,寬為內接正方形的邊長![]() .由劉徽構造的圖形還可以得到許多重要的結論,如圖3.設
.由劉徽構造的圖形還可以得到許多重要的結論,如圖3.設![]() 為斜邊
為斜邊![]() 的中點,作直角三角形
的中點,作直角三角形![]() 的內接正方形對角線
的內接正方形對角線![]() ,過點
,過點![]() 作
作![]() 于點
于點![]() ,則下列推理正確的是( )
,則下列推理正確的是( )
①由圖1和圖2面積相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得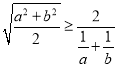 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:高中數學 來源: 題型:
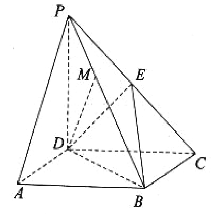
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上的一點.
上的一點.
(1)若![]() 平面
平面![]() ,證明:
,證明:![]() ;
;
(2)在(1)的條件下,棱![]() 上是否存在點
上是否存在點![]() ,使直線
,使直線![]() 與平面
與平面![]() 所成角的大小為
所成角的大小為![]() ?若存在,求
?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于![]() 的說法,正確的是( )
的說法,正確的是( )
A.展開式中的二項式系數之和為2048
B.展開式中只有第6項的二項式系數最大
C.展開式中第6項和第7項的二項式系數最大
D.展開式中第6項的系數最小
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 為常數,函數
為常數,函數![]() .給出以下結論:
.給出以下結論:
①若![]() ,則
,則![]() 在區間
在區間![]() 上有唯一零點;
上有唯一零點;
②若![]() ,則存在實數
,則存在實數![]() ,當
,當![]() 時,
時,![]()
![]() ;
;
③若![]() ,則當
,則當![]() 時,
時,![]() .
.
其中正確結論的個數是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com