
給出下列四個命題,其中不正確命題的序號是 。
①若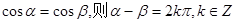 ;②函數
;②函數 的圖象關于x=
的圖象關于x= 對稱;③函數
對稱;③函數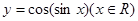 為偶函數,④函數
為偶函數,④函數 是周期函數,且周期為2
是周期函數,且周期為2 。
。
①②④
解析試題分析:由誘導公式,我們根據cosα=cosβ可判斷①的真假;根據余弦函數的對稱性,可判斷②的真假;根據函數奇偶性的定義,可判斷③的真假;根據函數周期性可以判斷④的真假,進而得到答案.解:若cosα=cosβ,則α-β=2kπ,或α+β=2kπ,k∈Z,故①不正確;函數y=2cos(2x+ )的圖象關于(
)的圖象關于( ,0)中心對稱,故②不正確;由函數f(-x)=cos[sin(-x)]=cos(sinx)(x∈R),故f(x)為偶函數,故③正確;函數y=sin|x|是周期函數,且周期為π,故④不正確.故答案為:①②④
,0)中心對稱,故②不正確;由函數f(-x)=cos[sin(-x)]=cos(sinx)(x∈R),故f(x)為偶函數,故③正確;函數y=sin|x|是周期函數,且周期為π,故④不正確.故答案為:①②④
考點:命題的真假判斷,三角函數的周期性
點評:本題考查的知識點是命題的真假判斷與應用,三角函數的周期性及其求法,余弦函數的奇偶性,余弦函數的對稱性,熟練掌握三角函數的性質是解答本題的關鍵


科目:高中數學 來源: 題型:填空題
下列說法:
①“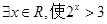 ”的否定是“
”的否定是“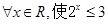 ”;
”;
②函數 的最小正周期是
的最小正周期是
③命題“函數 處有極值,則
處有極值,則 ”的否命題是真命題;
”的否命題是真命題;
④ 上的奇函數,
上的奇函數, 時的解析式是
時的解析式是 ,則
,則 時的解析式為
時的解析式為 其中正確的說法是 。
其中正確的說法是 。
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
給出定義:若 (其中
(其中 為整數),則
為整數),則 叫做離實數
叫做離實數 最近的整數,記作
最近的整數,記作 ,即
,即 . 在此基礎上給出下列關于函數
. 在此基礎上給出下列關于函數 的四個命題:
的四個命題:
① 的定義域是
的定義域是 ,值域是
,值域是 ;
;
②點 是
是 的圖像的對稱中心,其中
的圖像的對稱中心,其中 ;
;
③函數 的最小正周期為
的最小正周期為 ;
;
④ 函數 在
在 上是增函數.
上是增函數.
則上述命題中真命題的序號是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com