
【題目】已知直線![]() 與函數
與函數![]() (
(![]() )的圖象相交,將其中三個相鄰交點從左到右依次記為A,B,C,且滿足
)的圖象相交,將其中三個相鄰交點從左到右依次記為A,B,C,且滿足![]()
![]() 有下列結論:
有下列結論:
①n的值可能為2
②當![]() ,且
,且![]() 時,
時,![]() 的圖象可能關于直線
的圖象可能關于直線![]() 對稱
對稱
③當![]() 時,有且僅有一個實數ω,使得
時,有且僅有一個實數ω,使得![]() 在
在![]() 上單調遞增;
上單調遞增;
④不等式![]() 恒成立
恒成立
其中所有正確結論的編號為( )
A.③B.①②C.②④D.③④
【答案】D
【解析】
根據三角函數的圖像性質,依次分析四個結論即可求解.
解析:如圖所示,
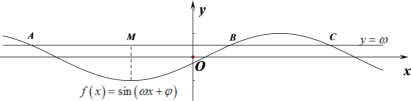
不妨設![]() ,
,![]() ,
,![]() ,且線段
,且線段![]() 的中點為
的中點為![]() ,
,
顯然有![]() ,
,![]() ,且
,且![]() 的圖象關于直線
的圖象關于直線![]() 對稱,
對稱,
∵![]()
![]() ,∴
,∴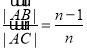
![]() ,
,
∴![]() ,即
,即![]() ,(1)
,(1)
∵![]() ,且
,且![]() ,∴由正弦曲線的圖像可知,
,∴由正弦曲線的圖像可知,
![]() (
(![]() ).
).
∴![]() (
(![]() ),
),
即![]() ,(2)
,(2)
由等式(1),(2)可得![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,且
,且![]() ,∴
,∴![]() ,且
,且![]() ,
,
對于結論①,顯然![]() ,故結論①錯誤:
,故結論①錯誤:
對于結論②,當![]() ,且
,且![]() 時,則
時,則![]() ,
,
故![]() ,若
,若![]() 的圖象關于直線
的圖象關于直線![]() 對稱,
對稱,
則![]() (
(![]() ),即
),即![]() (
(![]() )
)
顯然與![]() 矛盾,從而可知結論②錯誤:
矛盾,從而可知結論②錯誤:
對于結論③,∵![]() ,且
,且![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
∴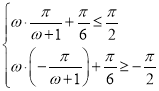 ,∴
,∴![]() ,故結論③正確;
,故結論③正確;
對于結論④,下證不等式![]() (
(![]() ),
),
(法一)當![]() 時,
時,![]() ,
,
∴![]() (
(![]() ),即
),即![]() (
(![]() ),
),
(法二)即證不等式![]() (
(![]() )恒成立,
)恒成立,
構造函數![]() (
(![]() ),顯然函數
),顯然函數![]() 單調遞增,
單調遞增,
當![]() 時,
時,![]() ,即不等式
,即不等式![]() (
(![]() )恒成立,故結論④正確:
)恒成立,故結論④正確:
綜上所述,正確的結論編號為③④
故選:D


科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() 過點
過點![]() ,其參數方程為
,其參數方程為 (
(![]() 為參數,
為參數,![]() ),以
),以![]() 為極點,
為極點,![]() 軸非負半軸為極軸建立極坐標系,曲線
軸非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)求已知曲線![]() 和曲線
和曲線![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】田忌賽馬是《史記》中記載的一個故事,說的是齊國大將軍田忌經常與齊國眾公子賽馬,孫臏發現田忌的馬和其他人的馬相差并不遠,都分為上、中、下三等.于是孫臏給田忌將軍獻策:比賽即將開始時,他讓田忌用下等馬對戰公子們的上等馬,用上等馬對戰公子們的中等馬,用中等馬對戰公子們的下等馬,從而使田忌贏得了許多賭注.假設田忌的各等級馬與某公子的各等級馬進行一場比賽,田忌獲勝的概率如下表所示:
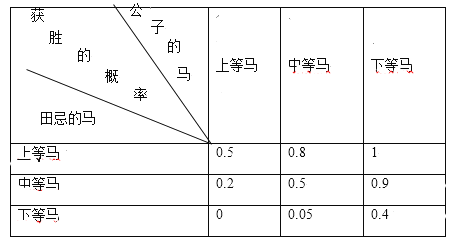
比賽規則規定:一次比賽由三場賽馬組成,每場由公子和田忌各出一匹馬參賽,結果只有勝和負兩種,并且毎一方三場賽馬的馬的等級各不相同,三場比賽中至少獲勝兩場的一方為最終勝利者.
(1)如果按孫臏的策略比賽一次,求田忌獲勝的概率;
(2)如果比賽約定,只能同等級馬對戰,每次比賽賭注1000金,即勝利者贏得對方1000金,每月比賽一次,求田忌一年賽馬獲利的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點F是拋物線![]() 的焦點,若點
的焦點,若點![]() 在拋物線C上,且
在拋物線C上,且![]()
(1)求拋物線C的方程;
(2)動直線![]() 與拋物線C相交于
與拋物線C相交于![]() 兩點,問:在x軸上是否存在定點
兩點,問:在x軸上是否存在定點![]() (其中
(其中![]() ),使得x軸平分
),使得x軸平分![]() ?若存在,求出點D的坐標;若不存在,請說明理由.
?若存在,求出點D的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓規是用來畫橢圓的一種器械,它的構造如圖所示,在一個十字形的金屬板上有兩條互相垂直的導槽,在直尺上有兩個固定的滑塊A,B,它們可分別在縱槽和橫槽中滑動,在直尺上的點M處用套管裝上鉛筆,使直尺轉動一周,則點M的軌跡C是一個橢圓,其中|MA|=2,|MB|=1,如圖,以兩條導槽的交點為原點O,橫槽所在直線為x軸,建立直角坐標系.
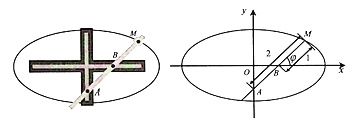
(1)將以射線Bx為始邊,射線BM為終邊的角xBM記為φ(0≤φ<2π),用![]() 表示點M的坐標,并求出C的普通方程;
表示點M的坐標,并求出C的普通方程;
(2)已知過C的左焦點F,且傾斜角為α(0≤α![]() )的直線l1與C交于D,E兩點,過點F且垂直于l1的直線l2與C交于G,H兩點.當
)的直線l1與C交于D,E兩點,過點F且垂直于l1的直線l2與C交于G,H兩點.當![]() ,|GH|,
,|GH|,![]() 依次成等差數列時,求直線l2的普通方程.
依次成等差數列時,求直線l2的普通方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定數列![]() .對
.對![]() ,該數列前
,該數列前![]() 項
項![]() 的最小值記為
的最小值記為![]() ,后
,后![]() 項
項![]() 的最大值記為
的最大值記為![]() ,令
,令![]() .
.
(1)設數列![]() 為2,1,6,3,寫出
為2,1,6,3,寫出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)設![]() 是等比數列,公比
是等比數列,公比![]() ,且
,且![]() ,證明:
,證明:![]() 是等比數列;
是等比數列;
(3)設![]() 是公差大于0的等差數列,且
是公差大于0的等差數列,且![]() ,證明:
,證明:![]() 是等差數列.
是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
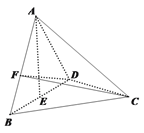
【題目】如圖,在三棱錐![]() 中,已知
中,已知![]() 都是邊長為
都是邊長為![]() 的等邊三角形,
的等邊三角形,![]() 為
為![]() 中點,且
中點,且![]() 平面
平面![]() ,
,![]() 為線段
為線段![]() 上一動點,記
上一動點,記![]() .
.
(1)當![]() 時,求異面直線
時,求異面直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(2)當![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com