
【題目】若![]() ,
, ![]() ,則實(shí)數(shù)
,則實(shí)數(shù)![]() 的取值范圍為__________.
的取值范圍為__________.
【答案】![]()
【解析】當(dāng)m=0時(shí),符合題意。
當(dāng)m≠0時(shí), ![]() ,則0<m<4,
,則0<m<4,
則0m<4
答案為: ![]() .
.
點(diǎn)睛:解本題的關(guān)鍵是處理二次函數(shù)在區(qū)間上大于0的恒成立問(wèn)題,對(duì)于二次函數(shù)的研究一般從以幾個(gè)方面研究:
一是,開(kāi)口;
二是,對(duì)稱軸,主要討論對(duì)稱軸與區(qū)間的位置關(guān)系;
三是,判別式,決定于x軸的交點(diǎn)個(gè)數(shù);
四是,區(qū)間端點(diǎn)值.
【題型】填空題
【結(jié)束】
15
【題目】已知橢圓![]() :
: ![]() 的右焦點(diǎn)為
的右焦點(diǎn)為![]() ,
, ![]() 為直線
為直線![]() 上一點(diǎn),線段
上一點(diǎn),線段![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,若
,若![]() ,則
,則![]() __________.
__________.

| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若關(guān)于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)設(shè)關(guān)于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ,集合
,集合![]() ,若
,若![]() ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系xOy中,曲線 ![]() ,曲線C2的參數(shù)方程為:
,曲線C2的參數(shù)方程為: ![]() ,(θ為參數(shù)),以O(shè)為極點(diǎn),x軸的正半軸為極軸的極坐標(biāo)系.
,(θ為參數(shù)),以O(shè)為極點(diǎn),x軸的正半軸為極軸的極坐標(biāo)系.
(1)求C1 , C2的極坐標(biāo)方程;
(2)射線 ![]() 與C1的異于原點(diǎn)的交點(diǎn)為A,與C2的交點(diǎn)為B,求|AB|.
與C1的異于原點(diǎn)的交點(diǎn)為A,與C2的交點(diǎn)為B,求|AB|.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為響應(yīng)黨中央“扶貧攻堅(jiān)”的號(hào)召,某單位指導(dǎo)一貧困村通過(guò)種植紫甘薯來(lái)提高經(jīng)濟(jì)收入.紫甘薯對(duì)環(huán)境溫度要求較高,根據(jù)以往的經(jīng)驗(yàn),隨著溫度的升高,其死亡株數(shù)成增長(zhǎng)的趨勢(shì).下表給出了2018年種植的一批試驗(yàn)紫甘薯在不同溫度時(shí)6組死亡的株數(shù):
溫度 | 21 | 23 | 24 | 27 | 29 | 32 |
死亡數(shù) | 6 | 11 | 20 | 27 | 57 | 77 |
經(jīng)計(jì)算:![]() ,
,![]() ,
,![]() ,
,![]() .
.
其中![]() 分別為試驗(yàn)數(shù)據(jù)中的溫度和死亡株數(shù),
分別為試驗(yàn)數(shù)據(jù)中的溫度和死亡株數(shù),![]() .
.
(1)![]() 與
與![]() 是否有較強(qiáng)的線性相關(guān)性? 請(qǐng)計(jì)算相關(guān)系數(shù)
是否有較強(qiáng)的線性相關(guān)性? 請(qǐng)計(jì)算相關(guān)系數(shù)![]() (精確到
(精確到![]() )說(shuō)明.
)說(shuō)明.
(2)并求![]() 關(guān)于
關(guān)于![]() 的回歸方程
的回歸方程![]() (
(![]() 和
和![]() 都精確到
都精確到![]() );
);
(3)用(2)中的線性回歸模型預(yù)測(cè)溫度為![]() 時(shí)該批紫甘薯死亡株數(shù)(結(jié)果取整數(shù)).
時(shí)該批紫甘薯死亡株數(shù)(結(jié)果取整數(shù)).
附:對(duì)于一組數(shù)據(jù)![]() ,
,![]() ,……,
,……,![]() ,
,
①線性相關(guān)系數(shù)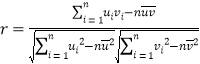 ,通常情況下當(dāng)
,通常情況下當(dāng)![]() 大于0.8時(shí),認(rèn)為兩
大于0.8時(shí),認(rèn)為兩
個(gè)變量有很強(qiáng)的線性相關(guān)性.
②其回歸直線![]() 的斜率和截距的最小二乘估計(jì)分別為:
的斜率和截距的最小二乘估計(jì)分別為:
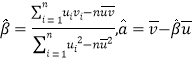 ;
;
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】紋樣是中國(guó)藝術(shù)寶庫(kù)的瑰寶,火紋是常見(jiàn)的一“種傳統(tǒng)紋樣.為了測(cè)算某火紋紋樣(如圖陰影部分所示)的面積,作一個(gè)邊長(zhǎng)為![]() 的正方形將其包含在內(nèi),并向該正方形內(nèi)隨機(jī)投擲
的正方形將其包含在內(nèi),并向該正方形內(nèi)隨機(jī)投擲![]() 個(gè)點(diǎn),已知恰有
個(gè)點(diǎn),已知恰有![]() 個(gè)點(diǎn)落在陰影部分,據(jù)此可估計(jì)陰影部分的面積是( )
個(gè)點(diǎn)落在陰影部分,據(jù)此可估計(jì)陰影部分的面積是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知二次函數(shù)![]() 同時(shí)滿足:①在定義域內(nèi)存在
同時(shí)滿足:①在定義域內(nèi)存在![]() ,使得
,使得![]() 成立;
成立;
②不等式![]() 的解集有且只有一個(gè)元素;數(shù)列
的解集有且只有一個(gè)元素;數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,
,![]() ,
,![]() ,
,![]() 。
。
(Ⅰ)求![]() 的表達(dá)式;
的表達(dá)式;
(Ⅱ)求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅲ)設(shè)![]() ,
,![]() ,
,![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,若
,若![]() 對(duì)任意
對(duì)任意![]() ,且
,且![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com