Question

【題目】某校為了解一個英語教改實驗班的情況，舉行了一次測試，將該班30位學生的英語成績進行統計，得圖示頻率分布直方圖，其中成績分組區間是：[50，60），[60，70），[70，80），[80，90），[90，100]．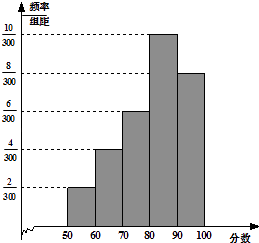

（1）求出該班學生英語成績的眾數，平均數及中位數；
（2）從成績低于80分的學生中隨機抽取2人，規定抽到的學生成績在[50，60）的記1績點分，在[60，80）的記2績點分，設抽取2人的總績點分為ξ，求ξ的分布列．

Answer 1

【答案】
（1）解：由頻率分布直方圖可知：眾數為85．

平均數為：55× =81，

∴該班學生英語成績的平均數為81．

設中位數為x，由頻率分布直方圖，得：

[50，80）內的頻率為（ ）×10=0.4，[80，90）內的頻率為 = ，

∴中位數x=80+ =83．

（2）解：依題意，成績在[50，60）的學生數為30× ，

成績在[60，80）的學生數為30× =10，

∴成績低于80分的學生總人數為 12，

∴ξ可取的值為2，3，4，

P（ξ=2）= = ，

P（ξ=3）= = ，

P（ξ=4）= = ，

∴ξ的分布列為：

ξ	2	3	4
P

∴ξ的數學期望E（ξ）=2× = ．

【解析】（1）由頻率分布直方圖能求出眾數、平均數和中位數．（2）依題意，成績在[50，60）的學生數為2人，成績在[60，80）的學生數為10人，ξ可取的值為2，3，4，分別求出相應的概率，由此能求出ξ的分布列和數學期望．
【考點精析】根據題目的已知條件，利用頻率分布直方圖和離散型隨機變量及其分布列的相關知識可以得到問題的答案，需要掌握頻率分布表和頻率分布直方圖，是對相同數據的兩種不同表達方式.用緊湊的表格改變數據的排列方式和構成形式，可展示數據的分布情況.通過作圖既可以從數據中提取信息，又可以利用圖形傳遞信息；在射擊、產品檢驗等例子中，對于隨機變量X可能取的值，我們可以按一定次序一一列出，這樣的隨機變量叫做離散型隨機變量．離散型隨機變量的分布列：一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn，X取每一個值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，則稱表為離散型隨機變量X 的概率分布，簡稱分布列．