
【題目】在△ABC中,D為BC邊上一點,BC=3BD,AD=![]() , ∠ADB=135°.若AC=
, ∠ADB=135°.若AC=![]() AB,則BD=
AB,則BD=
【答案】2+![]()
【解析】用余弦定理求得
AB2=BD2+AD2﹣2ADBDcos135°
AC2=CD2+AD2﹣2ADCDcos45°
即 AB2=BD2+2+2BD ①AC2=CD2+2﹣2CD ②
又BC=3BD
所以 CD=2BD
所以 由(2)得AC2=4BD2+2﹣4BD(3)
因為 AC=![]() AB
AB
所以 由(3)得 2AB2=4BD2+2﹣4BD (4)
(4)﹣2(1)
BD2﹣4BD﹣1=0
求得 BD=2+![]()
故答案為:2+![]()
先利用余弦定理可分別表示出AB,AC,把已知條件代入整理,根據BC=3BD推斷出CD=2BD,進而整理 AC2=CD2+2﹣2CD 得AC2=4BD2+2﹣4BD把AC=![]() AB,代入整理,最后聯立方程消去AB求得BD的方程求得BD.
AB,代入整理,最后聯立方程消去AB求得BD的方程求得BD.


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:高中數學 來源: 題型:
【題目】若關于x的不等式(a2﹣a)4x﹣2x﹣1<0在區間(﹣∞,1]上恒成立,則實數a的取值范圍為( )
A.(﹣2, ![]() )
)
B.(﹣∞, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣∞,6]
查看答案和解析>>
科目:高中數學 來源: 題型:
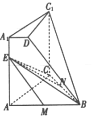
【題目】如圖,幾何體![]() 由一個正三棱柱截去一個三棱錐而得,
由一個正三棱柱截去一個三棱錐而得, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 為
為![]() 的中點,
的中點, ![]() 為棱
為棱![]() 上一點,且
上一點,且![]() 平面
平面![]() .
.
(1)若![]() 在棱
在棱![]() 上,且
上,且![]() ,證明:
,證明: ![]() 平面
平面![]() ;
;
(2)過![]() 作平面
作平面![]() 的垂線,垂足為
的垂線,垂足為![]() ,確定
,確定![]() 的位置(說明作法及理由),并求線段
的位置(說明作法及理由),并求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+bx+c,滿足f(1)=﹣![]() , 且3a>2c>2b.
, 且3a>2c>2b.
(1)求證:a>0時,![]() 的取值范圍;
的取值范圍;
(2)證明函數f(x)在區間(0,2)內至少有一個零點;
(3)設x1 , x2是函數f(x)的兩個零點,求|x1﹣x2|的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,A,B是海面上位于東西方向相距5(3+![]() )海里的兩個觀測點,現位于A點北偏東45°,B點北偏西60°的D點有一艘輪船發出求救信號,位于B點南偏西60°且與B點相距20
)海里的兩個觀測點,現位于A點北偏東45°,B點北偏西60°的D點有一艘輪船發出求救信號,位于B點南偏西60°且與B點相距20![]() 海里的C點的救援船立即即前往營救,其航行速度為30海里/小時,該救援船到達D點需要多長時間?
海里的C點的救援船立即即前往營救,其航行速度為30海里/小時,該救援船到達D點需要多長時間?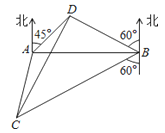
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】5個球放入3個盒子,在下列不同條件下,各有多少種投放方法?
①小球不同,盒子不同,盒子不空
②小球不同,盒子不同,盒子可空
③球不同,盒子相同,盒子不空
④小球不同,盒子相同,盒子可空
⑤小球相同,盒子不同,盒子不空
⑥小球相同,盒子不同,盒子可空
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為增強市民的環保意識,某市面向全市增招環保知識義務宣傳志愿者,從符合條件的志愿者中隨機選取![]() 名志愿者,其年齡頻率分布直方圖如圖所示,其中年齡(歲)分成五組:第
名志愿者,其年齡頻率分布直方圖如圖所示,其中年齡(歲)分成五組:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,得到的頻率分布直方圖(局部)如圖所示.
,得到的頻率分布直方圖(局部)如圖所示.
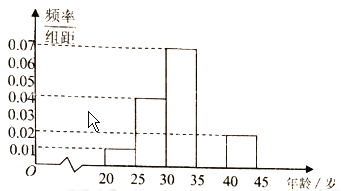
(1)求第![]() 組的頻率,并在圖中補畫直方圖;
組的頻率,并在圖中補畫直方圖;
(2)從![]() 名志愿者中再選出年齡低于
名志愿者中再選出年齡低于![]() 歲的志愿者
歲的志愿者![]() 名擔任主要宣講人,求這
名擔任主要宣講人,求這![]() 名主要宣講人的年齡在不同一組的概率.
名主要宣講人的年齡在不同一組的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com