
【題目】已知向量 ![]() =(2sinx,
=(2sinx, ![]() cosx),
cosx), ![]() =(﹣sinx,2sinx),函數f(x)=
=(﹣sinx,2sinx),函數f(x)= ![]()
![]() .
.
(1)求f(x)的單調遞增區間;
(2)求函數f(x)在區間[0, ![]() ]的最值及所對應的x值.
]的最值及所對應的x值.
【答案】
(1)解:向量 ![]() =(2sinx,
=(2sinx, ![]() cosx),
cosx), ![]() =(﹣sinx,2sinx),
=(﹣sinx,2sinx),
函數f(x)= ![]()
![]()
=﹣2sin2x+2 ![]() sinxcosx
sinxcosx
=﹣2× ![]() +
+ ![]() sin2x
sin2x
= ![]() sin2x+cos2x﹣1
sin2x+cos2x﹣1
=2sin(2x+ ![]() )﹣1;
)﹣1;
根據正弦函數的圖象與性質,
令﹣ ![]() +2kπ≤2x+
+2kπ≤2x+ ![]() ≤
≤ ![]() +2kπ,k∈Z,
+2kπ,k∈Z,
解得﹣ ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,k∈Z,
+kπ,k∈Z,
所以函數f(x)的單調遞增區間是[﹣ ![]() +kπ,
+kπ, ![]() +kπ],k∈Z
+kπ],k∈Z
(2)解:當x∈[0, ![]() ]時,2x+
]時,2x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
所以sin(2x+ ![]() )∈[﹣
)∈[﹣ ![]() ,1],
,1],
所以sin(2x+ ![]() )﹣1∈[﹣
)﹣1∈[﹣ ![]() ,0],
,0],
所以當x= ![]() 時,函數f(x)在區間[0,
時,函數f(x)在區間[0, ![]() ]上取得最小值﹣
]上取得最小值﹣ ![]() ,
,
x= ![]() 時,函數f(x)取得最大值0
時,函數f(x)取得最大值0
【解析】根據平面向量的數量積求出f(x)的解析式,(1)根據正弦函數的圖象與性質,求出函數f(x)的單調遞增區間;(2)求出x∈[0, ![]() ]時sin(2x+
]時sin(2x+ ![]() )的取值,從而求出函數f(x)在區間[0,
)的取值,從而求出函數f(x)在區間[0, ![]() ]上的最值以及對應x的值.
]上的最值以及對應x的值.
【考點精析】關于本題考查的正弦函數的單調性,需要了解正弦函數的單調性:在![]()
![]() 上是增函數;在
上是增函數;在![]()
![]() 上是減函數才能得出正確答案.
上是減函數才能得出正確答案.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知f(x)=x2+px+q.求證:
(1)f(1)+f(3)-2f(2)=2;
(2)|f(1)|,|f(2)|,|f(3)|中至少有一個不小于![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有一塊扇形鐵皮OAB,∠AOB=60°,OA=72cm,要剪下來一個扇環形ABCD,作圓臺容器的側面,并且在余下的扇形OCD內能剪下一塊與其相切的圓形使它恰好作圓臺容器的下底面(大底面).試求:
(1)AD應取多長?
(2)容器的容積為多大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在2008奧運會上兩名射擊運動員甲、乙在比賽中打出如下成績:甲:9.4,8.7,7.5,8.4,10.1,10.5,10.7,7.2,7.8,10.8;乙:9.1,8.7,7.1,9.8,9.7,8.5,10.1,9.2,10.1,9.1;用莖葉圖表示甲,乙兩個成績;并根據莖葉圖分析甲、乙兩人成績如圖所示,莖表示成績的整數環數,葉表示小數點后的數字.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數g(x)=ax﹣ ![]() ﹣5lnx,其中a∈R.
﹣5lnx,其中a∈R.
(1)若g(x)在其定義域內為增函數,求正實數a的取值范圍;
(2)設函數h(x)=x2﹣mx+4,當a=2時,若x1∈(0,1),x2∈[1,2],總有g(x1)≥h(x2)成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,以等腰直角三角形ABC的斜邊BC上的高AD為折痕,把△ABD和△ACD折成互相垂直的兩個平面后,某學生得出下列四個結論:
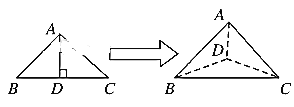
①BD⊥AC; ②△BAC是等邊三角形;
③三棱錐D-ABC是正三棱錐; ④平面ADC⊥平面ABC。
其中正確的是___________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ln(1+x)﹣ ![]() (a>0)
(a>0)
(1)若x=1是函數f(x)的一個極值點,求a的值;
(2)若f(x)≥0在[0,+∞)上恒成立,求a的取值范圍;
(3)證明: ![]() (e為自然對數的底數).
(e為自然對數的底數).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex(x2﹣2x+2﹣a2)(a>0),g(x)=x2+6x+c(c∈R).
(1)若曲線y=f(x)在點(0,f(0))處的切線方程為y=﹣4x﹣2,求a的值;
(2)求函數f(x)的單調區間;
(3)當a=1時,對x1∈[﹣2,2],x2∈[﹣2,2],使f(x1)<g(x2)成立,求實數c的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com