
【題目】在四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 為等邊三角形,
為等邊三角形,![]() ,
,![]() ,
,![]() ,點
,點![]() 是
是![]() 的中點.
的中點.
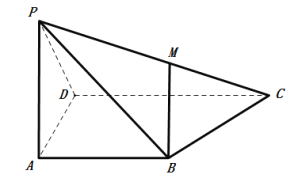
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析(2)![]()
【解析】
(1)取![]() 中點
中點![]() ,連結(jié)
,連結(jié)![]() ,
,![]() ,證明四邊形
,證明四邊形![]() 為平行四邊形得到答案.
為平行四邊形得到答案.
(2)證明![]() 平面
平面![]() ,如圖建立空間直角坐標(biāo)系,平面
,如圖建立空間直角坐標(biāo)系,平面![]() 的法向量
的法向量![]() ,面
,面![]() 的法向量
的法向量![]() ,計算夾角得到答案.
,計算夾角得到答案.
(1)取![]() 中點
中點![]() ,連結(jié)
,連結(jié)![]() ,
,![]() .
.
因為![]() 為
為![]() 中點,所以
中點,所以![]() ,
,![]() .
.
因為![]() ,
,![]() .所以
.所以![]() 且
且![]() .
.
所以四邊形![]() 為平行四邊形,所以
為平行四邊形,所以![]() .
.
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
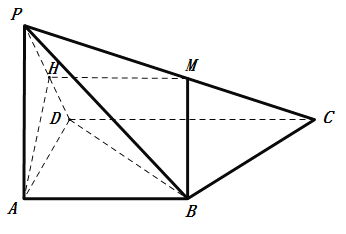
(2)取![]() 中點
中點![]() ,連結(jié)
,連結(jié)![]() .因為
.因為![]() ,所以
,所以![]() .
.
因為平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,取
,取![]() 中點
中點![]() ,連結(jié)
,連結(jié)![]() ,
,
則![]() .以
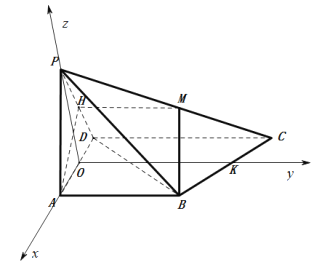
.以![]() 為原點,如圖建立空間直角坐標(biāo)系,
為原點,如圖建立空間直角坐標(biāo)系,
由![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .平面
.平面![]() 的法向量
的法向量![]() ,
,
設(shè)平面![]() 的法向量
的法向量![]() ,由
,由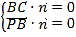 ,得
,得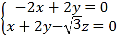 .
.
令![]() ,則
,則![]() ,
,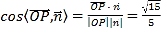 .由圖可知,
.由圖可知,
二面角![]() 是銳二面角,所以二面角
是銳二面角,所以二面角![]() 的余弦值為
的余弦值為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】推進(jìn)垃圾分類處理,是落實綠色發(fā)展理念的必然選擇,也是打贏污染防治攻堅戰(zhàn)的重要環(huán)節(jié).為了解居民對垃圾分類的了解程度某社區(qū)居委會隨機抽取1000名社區(qū)居民參與問卷測試,并將問卷得分繪制頻率分布表如表:
得分 | [30,40) | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
男性人數(shù) | 40 | 90 | 120 | 130 | 110 | 60 | 30 |
女性人數(shù) | 20 | 50 | 80 | 110 | 100 | 40 | 20 |
(1)從該社區(qū)隨機抽取一名居民參與問卷測試試估計其得分不低于60分的概率:
(2)將居民對垃圾分類的了解程度分為“比較了解”(得分不低于60分)和“不太了解”(得分低于60)兩類,完成2×2列聯(lián)表,并判斷是否有95%的把握認(rèn)為“居民對垃圾分類的了解程度”與“性別”有關(guān)?
不太了解 | 比較了解 | 合計 | |
男性 | |||
女性 | |||
合計 |
(3)從參與問卷測試且得分不低于80分的居民中,按照性別進(jìn)行分層抽樣,共抽取10人,現(xiàn)從這10人中隨機抽取3人作為環(huán)保宣傳隊長,設(shè)3人中男性隊長的人數(shù)為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附:![]() .
.
臨界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于函數(shù)![]() ,若存在區(qū)間
,若存在區(qū)間![]() ,使得
,使得![]() ,則稱函數(shù)
,則稱函數(shù)![]() 為“可等域函數(shù)”,區(qū)間A為函數(shù)的一個“可等域區(qū)間”.給出下列四個函數(shù):①
為“可等域函數(shù)”,區(qū)間A為函數(shù)的一個“可等域區(qū)間”.給出下列四個函數(shù):①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中存在唯一“可等域區(qū)間”的“可等域函數(shù)”的個數(shù)是( )
.其中存在唯一“可等域區(qū)間”的“可等域函數(shù)”的個數(shù)是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,已知ABCD為梯形,AB∥CD,CD=2AB,M為線段PC上一點.
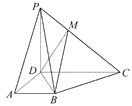
(1)設(shè)平面PAB∩平面PDC=l,證明:AB∥l;
(2)在棱PC上是否存在點M,使得PA∥平面MBD,若存在,請確定點M的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且橢圓上一點與橢圓的兩個焦點構(gòu)成的三角形周長為
,且橢圓上一點與橢圓的兩個焦點構(gòu)成的三角形周長為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設(shè)直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且以
兩點,且以![]() 為直徑的圓過橢圓的右頂點
為直徑的圓過橢圓的右頂點![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市堅持農(nóng)業(yè)與旅游融合發(fā)展,著力做好旅游各要素,完善旅游業(yè)態(tài),提升旅游接待能力.為了給游客提供更好的服務(wù),旅游部門需要了解游客人數(shù)的變化規(guī)律,收集并整理了![]() 年
年![]() 月至
月至![]() 年
年![]() 月期間月接待游客量(單位:萬人)的數(shù)據(jù),繪制了如圖所示的折線圖.根據(jù)該折線圖,下列結(jié)論正確的是( )
月期間月接待游客量(單位:萬人)的數(shù)據(jù),繪制了如圖所示的折線圖.根據(jù)該折線圖,下列結(jié)論正確的是( )
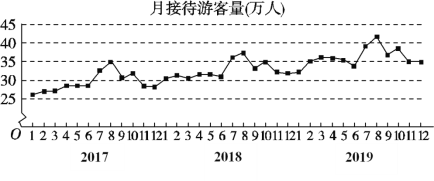
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相對于7月至12月,波動性更小,變化比較平穩(wěn)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】中國古代中的“禮、樂、射、御、書、數(shù)”合稱“六藝”.“禮”,主要指德育;“樂”,主要指美育;“射”和“御”,就是體育和勞動;“書”,指各種歷史文化知識;“數(shù)”,指數(shù)學(xué).某校國學(xué)社團(tuán)開展“六藝”課程講座活動,每藝安排一節(jié),連排六節(jié),一天課程講座排課有如下要求:“數(shù)”必須排在第三節(jié),且“射”和“御”兩門課程相鄰排課,則“六藝”課程講座不同的排課順序共有( )
A.12種B.24種C.36種D.48種
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的定義域為
的定義域為![]() ,若存在區(qū)間
,若存在區(qū)間![]() 使得
使得![]() :
:
(Ⅰ)![]() 在
在![]() 上是單調(diào)函數(shù);
上是單調(diào)函數(shù);
(Ⅱ)![]() 在
在![]() 上的值域是
上的值域是![]() ,
,
則稱區(qū)間![]() 為函數(shù)
為函數(shù)![]() 的“倍值區(qū)間”.
的“倍值區(qū)間”.
下列函數(shù)中存在“倍值區(qū)間”的有______________(填上所有你認(rèn)為正確的序號)
①![]() ; ②
; ②![]() ;
;
③![]() ; ④
; ④![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com