
已知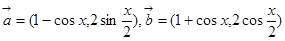 ,
,
設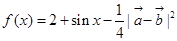 .
.
(Ⅰ)求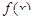 的表達式;
的表達式;
(Ⅱ)若函數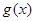 和函數
和函數 的圖象關于原點對稱,
的圖象關于原點對稱,
(ⅰ)求函數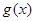 的解析式;
的解析式;
(ⅱ)若函數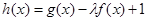 在區間
在區間 上是增函數,求實數l的取值范圍.
上是增函數,求實數l的取值范圍.
Ⅰ)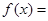
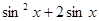 ;(Ⅱ)函數
;(Ⅱ)函數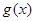 的解析式為
的解析式為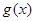 = -sin2x+2sinx ;
= -sin2x+2sinx ;
(Ⅲ)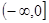 。
。
解析試題分析:(Ⅰ)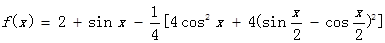
 4分
4分
(Ⅱ)設函數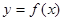 的圖象上任一點
的圖象上任一點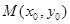 關于原點的對稱點為
關于原點的對稱點為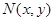
則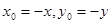 , .5分
, .5分
∵點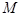 在函數
在函數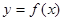 的圖象上
的圖象上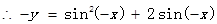 ,即
,即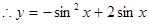
∴函數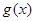 的解析式為
的解析式為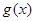 = -sin2x+2sinx 7分
= -sin2x+2sinx 7分
(Ⅲ)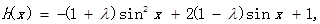
設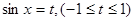 9分
9分
則有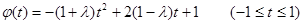
當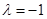 時,
時,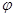 (t)=4t+1在[-1,1]上是增函數,∴λ= -1 11分
(t)=4t+1在[-1,1]上是增函數,∴λ= -1 11分
當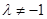 時,對稱軸方程為直線
時,對稱軸方程為直線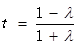 .
.
ⅰ) 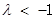 時,
時,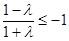 ,解得
,解得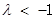
ⅱ)當 時,
時,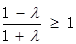 ,解得
,解得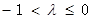
綜上: .
. 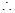 實數l的取值范圍為
實數l的取值范圍為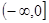 14分
14分
考點:本題主要考查平面向量的坐標運算,三角函數和差倍半公式的應用,二次函數圖象和性質。
點評:典型題,為研究三角函數的圖象和性質,往往需要將函數“化一”,這是常考題型。首先運用“三角公式”進行化簡,為進一步解題奠定了基礎。(3)小題利用“換元思想”,轉化成二次函數在閉區間的單調性研究問題,根據圖象對稱軸受到的限制,求得實數l的取值范圍。


 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:高中數學 來源: 題型:解答題
如圖,在半徑為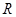 、圓心角為
、圓心角為 的扇形金屬材料中剪出一個長方形
的扇形金屬材料中剪出一個長方形 ,并且
,并且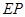 與
與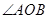 的平分線
的平分線 平行,設
平行,設 .
.
(1)試寫出用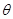 表示長方形
表示長方形 的面積
的面積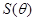 的函數;
的函數;
(2)在余下的邊角料中在剪出兩個圓(如圖所示),試問當矩形 的面積最大時,能否由這個矩形和兩個圓組成一個有上下底面的圓柱?如果可能,求出此時圓柱的體積.
的面積最大時,能否由這個矩形和兩個圓組成一個有上下底面的圓柱?如果可能,求出此時圓柱的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
如圖,用半徑為R的圓鐵皮,剪一個圓心角為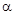 的扇形,制成一個圓錐形的漏斗,問圓心角
的扇形,制成一個圓錐形的漏斗,問圓心角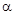 取什么值時,漏斗容積最大.(圓錐體積公式:
取什么值時,漏斗容積最大.(圓錐體積公式: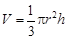 ,其中圓錐的底面半徑為r,高為h)
,其中圓錐的底面半徑為r,高為h)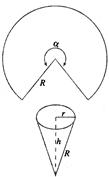
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com