
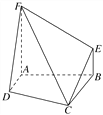
【題目】如圖,四邊形ABEF和四邊形ABCD均是直角梯形,∠FAB=∠DAB=90°,二面角FABD是直二面角,BE∥AF,BC∥AD,AF=AB=BC=2,AD=1.
(1)證明:在平面BCE上,一定存在過(guò)點(diǎn)C的直線l與直線DF平行;
(2)求二面角FCDA的余弦值.
【答案】(1)見(jiàn)解析(2)![]()
【解析】試題分析:(1)推導(dǎo)出平面BCE∥平面ADF.設(shè)平面DFC∩平面BCE=l,則l過(guò)點(diǎn)C.由平面BCE∥平面ADF,平面DFC∩平面BCE=l,得到DF∥l,由此能證明在平面BCE上一定存在過(guò)點(diǎn)C的直線l,使得DF∥l.(2)以A為原點(diǎn),AD,AB,AF分別為x軸,y軸,z軸建立空間直角坐標(biāo)系,利用向量法能求出二面角FCDA的余弦值.
試題解析:
(1)證明:由已知得,BE∥AF,BE平面AFD,AF平面AFD,
∴BE∥平面AFD.
同理可得,BC∥平面AFD.
又BE∩BC=B,∴平面BCE∥平面AFD.
設(shè)平面DFC∩平面BCE=l,則l過(guò)點(diǎn)C.
∵平面BCE∥平面ADF,平面DFC∩平面BCE=l,平面DFC∩平面AFD=DF,
∴DF∥l,即在平面BCE上一定存在過(guò)點(diǎn)C的直線l,使得DF∥l.
(2)∵平面ABEF⊥平面ABCD,平面ABCD∩平面ABEF=AB,FA平面ABEF,
又∠FAB=90°,∴AF⊥AB,∴AF⊥平面ABCD.
∵AD平面ABCD,∴AF⊥AD.
∵∠DAB=90°,∴AD⊥AB.
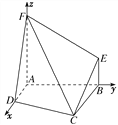
以A為坐標(biāo)原點(diǎn),AD,AB,AF所在直線分別為x軸,y軸,z軸建立如圖所示的空間直角坐標(biāo)系,由已知得,D(1,0,0),C(2,2,0),F(0,0,2),∴![]() =(-1,0,2),
=(-1,0,2),![]() =(1,2,0).
=(1,2,0).
設(shè)平面DFC的法向量為n=(x,y,z),
則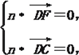 即
即![]()
令z=1,則n=(2,-1,1),
不妨取平面ACD的一個(gè)法向量為m=(0,0,1),
∴cos〈m,n〉=![]() =
=![]() =
=![]() ,
,
由于二面角FCDA為銳角,
因此二面角FCDA的余弦值為![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知離心率為![]() 的橢圓
的橢圓![]() 焦點(diǎn)在
焦點(diǎn)在![]() 軸上,且橢圓
軸上,且橢圓![]() 個(gè)頂點(diǎn)構(gòu)成的四邊形面積為
個(gè)頂點(diǎn)構(gòu)成的四邊形面積為![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于不同的兩點(diǎn)
相交于不同的兩點(diǎn)![]() 、
、![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)![]() 為橢圓上一點(diǎn),且
為橢圓上一點(diǎn),且![]() (
(![]() 為坐標(biāo)原點(diǎn)).求當(dāng)
為坐標(biāo)原點(diǎn)).求當(dāng)![]() 時(shí),實(shí)數(shù)
時(shí),實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,四棱錐![]() 的底面
的底面![]() 是矩形,側(cè)面
是矩形,側(cè)面![]() 是正三角形,
是正三角形,![]() ,
,![]() ,
,![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)若![]() 為
為![]() 中點(diǎn),求二面角
中點(diǎn),求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了展示中華漢字的無(wú)窮魅力,傳遞傳統(tǒng)文化,提高學(xué)習(xí)熱情,某校開(kāi)展《中國(guó)漢字聽(tīng)寫(xiě)大會(huì)》的活動(dòng).為響應(yīng)學(xué)校號(hào)召,2(9)班組建了興趣班,根據(jù)甲、乙兩人近期8次成績(jī)畫(huà)出莖葉圖,如圖所示(把頻率當(dāng)作概率).

(1)求甲、乙兩人成績(jī)的平均數(shù)和中位數(shù);
(2)現(xiàn)要從甲、乙兩人中選派一人參加比賽,從統(tǒng)計(jì)學(xué)的角度,你認(rèn)為派哪位學(xué)生參加比較合適?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在正三棱柱![]() 中,已知
中,已知![]() ,
,![]() 分別為
分別為![]() ,
,![]() 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)![]() 在棱
在棱![]() 上,且
上,且![]() .求證:
.求證:
(1)直線![]() ∥平面
∥平面![]() ;
;
(2)直線![]() 平面
平面![]() .
.

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,圓![]() :
:![]() .
.

(Ⅰ)若圓C與x軸相切,求圓C的方程;
(Ⅱ)已知![]() ,圓
,圓![]() 與x軸相交于兩點(diǎn)
與x軸相交于兩點(diǎn)![]() (點(diǎn)
(點(diǎn)![]() 在點(diǎn)
在點(diǎn)![]() 的左側(cè)).過(guò)點(diǎn)
的左側(cè)).過(guò)點(diǎn)![]() 任作一條直線與圓
任作一條直線與圓![]() :
:![]() 相交于兩點(diǎn)A,B.問(wèn):是否存在實(shí)數(shù)a,使得
相交于兩點(diǎn)A,B.問(wèn):是否存在實(shí)數(shù)a,使得![]() =
=![]() ?若存在,求出實(shí)數(shù)a的值,若不存在,請(qǐng)說(shuō)明理由.
?若存在,求出實(shí)數(shù)a的值,若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,島![]() 、
、![]() 相距
相距![]() 海里.上午9點(diǎn)整有一客輪在島
海里.上午9點(diǎn)整有一客輪在島![]() 的北偏西
的北偏西![]() 且距島
且距島![]()
![]() 海里的
海里的![]() 處,沿直線方向勻速開(kāi)往島
處,沿直線方向勻速開(kāi)往島![]() ,在島
,在島![]() 停留
停留![]() 分鐘后前往
分鐘后前往![]() 市.上午
市.上午![]() 測(cè)得客輪位于島
測(cè)得客輪位于島![]() 的北偏西
的北偏西![]() 且距島
且距島![]()
![]() 海里的
海里的![]() 處,此時(shí)小張從島
處,此時(shí)小張從島![]() 乘坐速度為
乘坐速度為![]() 海里/小時(shí)的小艇沿直線方向前往
海里/小時(shí)的小艇沿直線方向前往![]() 島換乘客輪去
島換乘客輪去![]() 市.
市.

(Ⅰ)若![]() ,問(wèn)小張能否乘上這班客輪?
,問(wèn)小張能否乘上這班客輪?
(Ⅱ)現(xiàn)測(cè)得![]() ,
, ![]() .已知速度為
.已知速度為![]() 海里/小時(shí)(
海里/小時(shí)(![]() )的小艇每小時(shí)的總費(fèi)用為(
)的小艇每小時(shí)的總費(fèi)用為(![]() )元,若小張由島
)元,若小張由島![]() 直接乘小艇去
直接乘小艇去![]() 市,則至少需要多少費(fèi)用?
市,則至少需要多少費(fèi)用?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在三棱錐S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,點(diǎn)E,F,G分別在棱SA,SB,SC上,且平面EFG∥平面ABC,點(diǎn)E為SA的中點(diǎn).求證:
(Ⅰ)AF⊥平面SBC;
(Ⅱ)SA⊥BC.

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】據(jù)統(tǒng)計(jì),某5家鮮花店今年4月的銷售額和利潤(rùn)額資料如下表:
鮮花店名稱 | A | B | C | D | E |
銷售額x(千元) | 3 | 5 | 6 | 7 | 9 |
利潤(rùn)額y(千元) | 2 | 3 | 3 | 4 | 5 |
(1)用最小二乘法計(jì)算利潤(rùn)額y關(guān)于銷售額x的回歸直線方程![]() =
=![]() x+
x+![]() ;
;
(2)如果某家鮮花店的銷售額為8千元時(shí),利用(1)的結(jié)論估計(jì)這家鮮花店的利潤(rùn)額是多少.
參考公式:回歸方程![]() 中斜率和截距的最小二乘法估計(jì)值公式分別為
中斜率和截距的最小二乘法估計(jì)值公式分別為
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com