
【題目】已知△DEF三邊所在的直線分別為l1:x=-2,l2:x+![]() y-4=0,l3:x-
y-4=0,l3:x-![]() y-4=0,⊙C為△DEF的內切圓.
y-4=0,⊙C為△DEF的內切圓.
(1)求⊙C的方程;
(2)設⊙C與x軸交于A、B兩點,點P在⊙C內,且滿足![]() .記直線PA、PB的斜率分別為k1、k2,求k1 k2的取值范圍.
.記直線PA、PB的斜率分別為k1、k2,求k1 k2的取值范圍.
【答案】(1)x2+y2=4.(2)(-1,0]
【解析】
(1)解法一:設C(a,b),⊙C半徑為r,則
![]() ,
,
結合點C(a,b)在△DEF內,可得![]() .
.
解得a=b=0,r=2.
∴⊙C的方程為x2+y2=4.
解法二:設C(a,b),⊙C半徑為r.
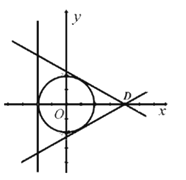
如圖,由條件知,l2、l3的傾斜角分別為150°和30°,且它們關于x軸對稱,同時l1⊥x軸.
因此,△DEF為正三角形.
∴點C在x軸上,且a=-2+r,b=0.
由l2、l3交x軸于點D(4,0),知△DEF的高為6.
∴![]() ,a=0.
,a=0.
∴⊙C的方程為x2+y2=4.
(2)由(1)知,C(0,0),A(-2,0),B(2,0).設P(x,y),則x2+y2<4.
∵![]() ,
,
∴![]() ,
,
化簡得,x2-y2=2.
∴![]() .
.
由x2+y2<4,以及x2-y2=2,y2≥0,得2≤x2<3.
∴k1 k2∈(-1,0].
∴k1 k2的取值范圍為(-1,0].


 快樂暑假暑假能力自測中西書局系列答案
快樂暑假暑假能力自測中西書局系列答案科目:高中數學 來源: 題型:
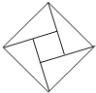
【題目】在北京召開的第24屆國際數學家大會會標如圖所示,它是由四個相同的直角三角形與中間的小正方形拼成的一個大正方形.若直角三角形中較小的銳角記作![]() ,大正方形的面積是1,小正方形的面積是
,大正方形的面積是1,小正方形的面積是![]() ,則
,則![]() 的值等于( )
的值等于( )
A. 1 B. ![]() C.
C. ![]()
![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設定義在(0,+∞)的單調函數f(x),對任意的x∈(0,+∞)都有f[f(x)﹣log2x]=6.若x0是方程f(x)﹣f′(x)=4的一個解,且 ![]() ,則a=( )
,則a=( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (其中
(其中![]() ),若
),若![]() 的一條對稱軸離最近的對稱中心的距離為
的一條對稱軸離最近的對稱中心的距離為![]() .
.
(Ⅰ)求![]() 的單調遞增區間;
的單調遞增區間;
(Ⅱ)在![]() 中角
中角![]() 、
、![]() 、
、![]() 的對邊分別是
的對邊分別是![]() 滿足
滿足![]() 恰是
恰是![]() 的最大值,試判斷
的最大值,試判斷![]() 的形狀.
的形狀.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C: ![]() 的焦點為F,直線
的焦點為F,直線![]() 與y軸的交點為P,與C的交點為Q,且
與y軸的交點為P,與C的交點為Q,且![]() .
.
(1)求C的方程;
(2)過F的直線![]() 與C相交于A,B兩點,若AB的垂直平分線
與C相交于A,B兩點,若AB的垂直平分線![]() 與C相較于M,N兩點,且A,M,B,N四點在同一圓上,求
與C相較于M,N兩點,且A,M,B,N四點在同一圓上,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合M={m|m∈Z,且|m|≤2018},M的子集S滿足:對S中任意3個元素a,b,c(不必不同),都有a+b+c≠0.求集合S的元素個數的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018河北保定市高三上學期期末調研】如圖,四面體![]() 中,
中, ![]() 、
、![]() 分別
分別![]() 、
、![]() 的中點,
的中點, ![]() ,
, ![]() .
.
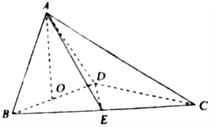
(I)求證: ![]() 平面
平面![]() ;
;
(II)求異面直線![]() 與
與![]() 所成角的余弦值的大小;
所成角的余弦值的大小;
(III)求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】高一數學競賽共設有35個考場,甲、乙、丙三所學校的領隊各自將本校學生人數相同的考場歸為一組.經統計,甲校共有i組,各組的考場數分別為![]() ;乙校共有j組,各組的考場數分別為
;乙校共有j組,各組的考場數分別為![]() ;丙校共有k組,各組的考場數分別為
;丙校共有k組,各組的考場數分別為![]() .已知
.已知![]() 包含了1 ~ 14的所有整數.證明:能找到三個考場,至少有兩所學校在這三個考場中的選手人數各自是相同的.
包含了1 ~ 14的所有整數.證明:能找到三個考場,至少有兩所學校在這三個考場中的選手人數各自是相同的.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com