C
分析:把集合M中的不等式左邊利用平方差公式分解因式,根據兩數相乘同號得正的取符號法則轉化為兩個一元一次不等式組,求出兩解集的并集確定出集合M,然后把集合M和N的解集表示在數軸上,找出兩集合的公共部分,即可得到兩集合的交集.
解答:由集合M中的不等式x
2-1>0,
變形得:(x+1)(x-1)>0,
可化為
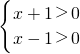
或
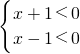
,
解得:x>1或x<-1,
∴集合M={x|x>1或x<-1},又N={x|x<2},
在數軸上畫出相應的解集,如圖所示:

則M∩N={x|1<x<2或x<-1}.
故選C
點評:此題考查了交集的運算,利用了轉化及數形結合的思想,其中確定出集合M,然后借助數軸,找出兩集合的公共部分是求交集的關鍵.

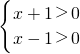 或
或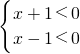 ,
,

