
【題目】如圖,四棱錐中, ![]() ,
, ![]()
![]()
![]() 側面
側面![]() 為等邊三角形,
為等邊三角形, ![]()
![]() ,
, ![]() 。
。

(1)證明: ![]() ;
;
(2)求二面角![]() 的平面角的正弦值。
的平面角的正弦值。
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:
(1)由題意可得![]() ,
, ![]() 結合線面垂直的判斷定理可得
結合線面垂直的判斷定理可得![]() ;
;
(2)首先找到二面角的平面角,然后結合幾何關系可得二面角![]() 的平面角的正弦值為
的平面角的正弦值為![]() .
.
試題解析:
(1) 解:取![]()
![]() 的中點
的中點![]()
![]() ,連結
,連結![]() ,
, ![]()
![]() ,則四邊形
,則四邊形![]()
![]() 為矩形。
為矩形。
即: ![]() ,
, ![]()
![]()
![]() ,
,
因為側面![]() 為等邊三角形,
為等邊三角形, ![]()
![]() ,所以
,所以![]() ,且
,且![]()
又因為![]() ,所以
,所以![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,而
,而![]() ,
, ![]() ,
, ![]() ,所以
,所以![]() 。
。
(2)![]()
![]() (2)過點
(2)過點![]()
![]() 作
作![]()
![]() 于
于![]() ,因為
,因為![]()
![]() ,
, ![]()
![]() ,所以
,所以![]() ,
,
又因為![]() ,即
,即![]() ,
,
由平面與平面垂直的性質,知![]() ,
,
在![]()
![]() 中,由
中,由![]()
![]() ,
,
得![]()
![]() ,所以
,所以![]()
![]() 。
。
過點![]()
![]() 作
作 ![]()
![]() 于
于![]() ,取
,取![]() 中點
中點![]() ,連結
,連結![]()
![]() ,
,
則![]()
![]() 為二面角
為二面角![]() 的平面角,
的平面角,
因為![]()
![]() ,
, ![]() ,所以
,所以![]()
![]() ,所以
,所以![]()
![]() ,
,
在![]()
![]() 中,由
中,由![]()
![]() ,求得
,求得![]()
![]() 。
。
在![]()
![]() 中,
中, ![]() ,
,![]() ,
,
所以![]() 。
。
由![]()
![]() ,得
,得![]()
![]() ,
,
即![]() ,解得
,解得![]() ,
,
![]() 所以
所以![]()
![]() ,
,
故二面角![]() 的平面角的正弦值為
的平面角的正弦值為![]()
![]() 。
。


 培優三好生系列答案
培優三好生系列答案 優化作業上海科技文獻出版社系列答案
優化作業上海科技文獻出版社系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知圓
中,已知圓![]() 過坐標原點
過坐標原點![]() 且圓心在曲線
且圓心在曲線![]() 上.
上.
(1)若圓![]() 分別與
分別與![]() 軸、
軸、![]() 軸交于點
軸交于點![]() 、
、![]() (不同于原點
(不同于原點![]() ),求證:
),求證:![]() 的面積為定值;
的面積為定值;
(2)設直線![]() 與圓
與圓![]() 交于不同的兩點
交于不同的兩點![]() ,且
,且![]() ,求圓
,求圓![]() 的方程;
的方程;
(3)設直線![]() 與(2)中所求圓
與(2)中所求圓![]() 交于點
交于點![]() 、
、![]() ,
, ![]() 為直線
為直線![]() 上的動點,直線
上的動點,直線![]() ,
,![]() 與圓
與圓![]() 的另一個交點分別為
的另一個交點分別為![]() ,
,![]() ,且
,且![]() ,
,![]() 在直線
在直線![]() 異側,求證:直線
異側,求證:直線![]() 過定點,并求出定點坐標.
過定點,并求出定點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高中有高一新生500名,分成水平相同的![]() 兩類教學實驗,為對比教學效果,現用分層抽樣的方法從
兩類教學實驗,為對比教學效果,現用分層抽樣的方法從![]() 兩類學生中分別抽取了40人,60人進行測試
兩類學生中分別抽取了40人,60人進行測試
(1)求該學校高一新生![]() 兩類學生各多少人?
兩類學生各多少人?
(2)經過測試,得到以下三個數據圖表:
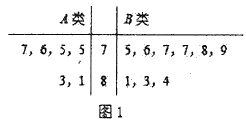
圖1:75分以上![]() 兩類參加測試學生成績的莖葉圖
兩類參加測試學生成績的莖葉圖
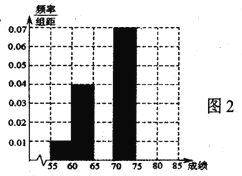
圖2:100名測試學生成績的頻率分布直方圖
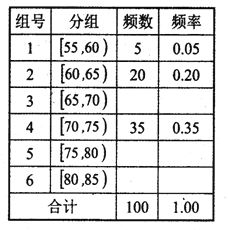
下圖表格:100名學生成績分布表:
①先填寫頻率分布表中的六個空格,然后將頻率分布直方圖(圖2)補充完整;
②該學校擬定從參加考試的79分以上(含79分)的![]() 類學生中隨機抽取2人代表學校參加市比賽,求抽到的2人分數都在80分以上的概率.
類學生中隨機抽取2人代表學校參加市比賽,求抽到的2人分數都在80分以上的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 為奇函數,且相鄰兩對稱軸間的距離為
為奇函數,且相鄰兩對稱軸間的距離為![]() .
.
(Ⅰ)當![]() 時,求
時,求![]() 的單調遞減區間;
的單調遞減區間;
(Ⅱ)將函數![]() 的圖象沿
的圖象沿![]() 軸方向向右平移
軸方向向右平移![]() 個單位長度,再把橫坐標縮短到原來的
個單位長度,再把橫坐標縮短到原來的![]() (縱坐標不變),
(縱坐標不變),
得到函數![]() 的圖象.當
的圖象.當![]() 時,求函數
時,求函數![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在坐標原點,左、右焦點
的中心在坐標原點,左、右焦點![]() 分別在
分別在![]() 軸上,離心率為
軸上,離心率為![]() ,在其上有一動點
,在其上有一動點![]() ,
,![]() 到點
到點![]() 距離的最小值是1.過
距離的最小值是1.過![]() 作一個平行四邊形,頂點
作一個平行四邊形,頂點![]() 都在橢圓
都在橢圓![]() 上,如圖所示.
上,如圖所示.

(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)判斷![]() 能否為菱形,并說明理由.
能否為菱形,并說明理由.
(Ⅲ)當![]() 的面積取到最大值時,判斷
的面積取到最大值時,判斷![]() 的形狀,并求出其最大值.
的形狀,并求出其最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代數學成就的杰出代表,其中《方田》章有弧田面積計算問題,計算術曰:以弦乘矢,矢又自乘,并之,二而一.其大意是,弧田面積計算公
式為:弧田面積=![]() ,弧田是由圓弧(簡稱為弧田弧)和以圓
,弧田是由圓弧(簡稱為弧田弧)和以圓
弧的兩端為頂點的線段(簡稱為弧田弦)圍成的平面圖形,公式中“弦”指的是弧
田弦的長,“矢”等于弧田弧所在圓的半徑與圓心到弧田弦的距離之差.現有一弧
田,其弦長AB等于6米,其弧所在圓為圓O,若用上述弧田面積計算公式算得該
弧田的面積為![]() 平方米,則cos∠AOB= ( )
平方米,則cos∠AOB= ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小王、小李兩位同學玩擲骰子(骰子質地均勻)游戲,規則:小王先擲一枚骰子,向上的點數記為![]() ;小李后擲一枚骰子,向上的點數記為
;小李后擲一枚骰子,向上的點數記為![]() .
.
(1)求![]() 能被
能被![]() 整除的概率.
整除的概率.
(2)規定:若![]() ,則小王贏;若
,則小王贏;若![]() ,則小李贏,其他情況不分輸贏.試問這個游戲規則公平嗎?請說明理由.
,則小李贏,其他情況不分輸贏.試問這個游戲規則公平嗎?請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com