
【題目】已知集合P={x∈R|x2-3x+b=0},Q={x∈R|(x+1)(x2+3x-4)=0}.
(1)若b=4,存在集合M使得P![]() M
M![]() Q;
Q;
(2)若PQ,求b的取值范圍.
【答案】(1)詳見解析(2)(![]() ,+∞)
,+∞)
【解析】
(1)由于集合Q={-1,1,-4},當b=4時,集合P=,再由 P![]() MQ可得,M是Q的非空子集,從而得到M.
MQ可得,M是Q的非空子集,從而得到M.
(2)當P=,△=9-4b<0時,有.當P≠,方程x2-3x+b=0有實數根,且實數根是-1,1,-4中的數,把x=-1,1,-4代入檢驗,由此得到實數b的取值范圍.
解:(1)∵集合Q={x|(x+1)(x2+3x-4)=0}={x|(x+1)(x+4)(x-1)=0}={-1,1,-4},
當b=4時,集合P=,再由P ![]() MQ可得,M是Q的非空子集.
MQ可得,M是Q的非空子集.
共有23-1=7 個,分別為{-1}、{1}、{-4}、{-1,1}、{-1,4}、{1,4}、{-1,1,-4}.
(2)∵PQ,對于方程x2-3x+b=0,
當P=,△=9-4b<0時,有b>![]() ,
,
△=9-4b≥0時,P≠,方程x2-3x+b=0有實數根,且實數根是-1,1,-4中的數.
若-1是方程x2-3x+b=0的實數根,則有b=-4,此時P={-1,4},不滿足PQ,故舍去.
若1是方程x2-3x+b=0的實數根,則有b=2,此時P={1,2},不滿足PQ,故舍去.
若-4是方程x2-3x+b=0的實數根,則有b=2,此時P={-1,4},不滿足PQ,故舍去.
綜上可得,實數b的取值范圍為(![]() ,+∞).
,+∞).


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C的焦點坐標是F1(﹣1,0)、F2(1,0),過點F2垂直于長軸的直線l交橢圓C于B、D兩點,且|BD|=3.
(1)求橢圓C的方程;
(2)過定點P(0,2)且斜率為k的直線l與橢圓C相交于不同兩點M,N,試判斷:在x軸上是否存在點A(m,0),使得以AM,AN為鄰邊的平行四邊形為菱形?若存在,求出實數m的取值范圍,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知公比小于1的等比數列{an}的前n項和為Sn , a1= ![]() 且13a2=3S3(n∈N*).
且13a2=3S3(n∈N*).
(1)求數列{an}的通項公式;
(2)設bn=nan , 求數列{bn}的前項n和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖, ![]() 為坐標原點,橢圓
為坐標原點,橢圓![]()
![]() 的左右焦點分別為
的左右焦點分別為![]() ,離心率為
,離心率為![]() ;雙曲線
;雙曲線![]()
![]() 的左右焦點分別為
的左右焦點分別為![]() ,離心率為
,離心率為![]() ,已知
,已知![]() ,且
,且![]() .
.
(1)求![]() 的方程;
的方程;
(2)過![]() 點作
點作![]() 的不垂直于
的不垂直于![]() 軸的弦
軸的弦![]() ,
, ![]() 為
為![]() 的中點,當直線
的中點,當直線![]() 與
與![]() 交于
交于![]() 兩點時,求四邊形
兩點時,求四邊形![]() 面積的最小值.
面積的最小值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩個班級共有105名學生,某次數學考試按照“大于等于85分為優秀,85分以下為非優秀”的原則統計成績后,得到如下![]() 列聯表。
列聯表。
優秀 | 非優秀 | 總計 | |
甲班 | 10 | ||
乙班 | 30 | ||
總計 | 105 |
已知從甲、乙兩個班級中隨機抽取1名學生,其成績為優秀的概率為![]() .
.
(1)請完成上面的![]() 列聯表;
列聯表;
(2)能否有把握認為成績與班級有關系?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點 ![]() 在橢圓
在橢圓 ![]() 上,過橢圓C的右焦點F且垂直于橢圓長軸的弦長為3.
上,過橢圓C的右焦點F且垂直于橢圓長軸的弦長為3.
(1)求橢圓C的方程;
(2)若MN是過橢圓C的右焦點F的動弦(非長軸),點T為橢圓C的左頂點,記直線TM,TN的斜率分別為k1 , k2 . 問k1k2是否為定值?若為定值,請求出定值;若不為定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】響應“文化強國建設”號召,某市把社區圖書閱覽室建設增列為重要的民生工程.為了解市民閱讀需求,隨機抽取市民200人做調查,統計顯示,男士喜歡閱讀古典文學的有64人,不喜歡的有56人;女士喜歡閱讀古典文學的有36人,不喜歡的有44人.
(1)能否在犯錯誤的概率不超過0.25的前提下認為喜歡閱讀古典文學與性別有關系?
(2)為引導市民積極參與閱讀,有關部門牽頭舉辦市讀書交流會,從這200人中篩選出5名男代表和4名代表,其中有3名男代表和2名女代表喜歡古典文學.現從這9名代表中任選3名男代表和2名女代表參加交流會,記![]() 為參加交流會的5人中喜歡古典文學的人數,求
為參加交流會的5人中喜歡古典文學的人數,求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
附:![]() ,其中
,其中![]() .
.
參考數據:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中數學 來源: 題型:
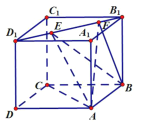
【題目】如圖所示,正方體![]() 的棱長為1,線段
的棱長為1,線段![]() 上有兩個動點
上有兩個動點![]() ,且
,且![]() ,則下列結論中正確的是__________.
,則下列結論中正確的是__________.
①![]() 平面
平面![]() ;
;
②平面![]() 平面
平面![]() ;
;
③三棱錐![]() 的體積為定值;
的體積為定值;
④存在某個位置使得異面直線![]() 與
與![]() 成角
成角![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com