
【題目】
已知函數![]() (
(![]() 是自然對數的底數).
是自然對數的底數).
(1)若曲線![]() 在
在![]() 處的切線也是拋物線
處的切線也是拋物線![]() 的切線,求
的切線,求![]() 的值;
的值;
(2)若對于任意![]() 恒成立,試確定實數
恒成立,試確定實數![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,是否存在
時,是否存在![]() ,使曲線
,使曲線![]() 在點
在點![]() 處的切線斜率與
處的切線斜率與![]() 在
在![]() 上的最小值相等?若存在,求符合條件的
上的最小值相等?若存在,求符合條件的![]() 的個數;若不存在,請說明理由.
的個數;若不存在,請說明理由.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() (3)相等,一個.
(3)相等,一個.
【解析】
(1)求出![]() 在
在![]() 的切線,與
的切線,與![]() 聯立,根據切線與拋物線只有一個交點,則
聯立,根據切線與拋物線只有一個交點,則![]() ;(2)分
;(2)分![]() ,
,![]() ,
,![]() 根據導數討論;(3)轉化為函數的零點通過導數求解.
根據導數討論;(3)轉化為函數的零點通過導數求解.
(1)![]() ,
,
所以在![]() 處的切線為
處的切線為![]()
即:![]()
與![]() 聯立,消去
聯立,消去![]() 得
得![]() ,
,
由![]() 知,
知,![]() 或
或![]()
(2)![]()
①當![]() 時,
時,![]() 在
在![]() 上單調遞增,且當
上單調遞增,且當![]() 時,
時,![]() ,
,
![]() ,故
,故![]() 不恒成立,所以
不恒成立,所以![]() 不合題意 ;
不合題意 ;
②當![]() 時,
時,![]() 對
對![]() 恒成立,所以
恒成立,所以![]() 符合題意;
符合題意;
③當![]() 時令
時令![]() ,得
,得![]() ,
,
當![]() 時,
時,![]() ,
,
當![]() 時,
時,![]() ,
,
故![]() 在
在![]() 上是單調遞減,在
上是單調遞減,在![]() 上是單調遞增,
上是單調遞增,
所以![]()
![]() 又
又![]() ,
,![]() ,
,
綜上:![]()
(3)當![]() 時,
時,
由(2)知![]() ,
,
設![]() ,
,
則![]() ,
,
假設存在實數![]() ,使曲線
,使曲線![]() 在點
在點![]() 處的切線斜率與
處的切線斜率與![]() 在
在![]() 上的最小值相等,
上的最小值相等,![]() 即為方程的解,
即為方程的解,
令![]() 得:
得:![]() ,
,
因為![]() , 所以
, 所以![]() .
.
令![]() ,則
,則![]() ,
,
當![]() 是
是![]() ,當
,當![]() 時
時![]() ,
,
所以![]() 在
在![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增,
上單調遞增,
![]() ,故方程
,故方程![]() 有唯一解為1,
有唯一解為1,
所以存在符合條件的![]() ,且僅有一個
,且僅有一個![]() .
.


 教學練新同步練習系列答案
教學練新同步練習系列答案科目:高中數學 來源: 題型:
【題目】高二某班共有45人,學號依次為1、2、3、…、45,現按學號用系統抽樣的辦法抽取一個容量為5的樣本,已知學號為6、24、33的同學在樣本中,那么樣本中還有兩個同學的學號應為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx+2x﹣1.
(1)求f(x)的極值;
(2)若對任意的x>1,都有f(x)﹣k(x﹣1)>0(k∈Z)恒成立,求k的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】居民消費價格指數,簡稱CPI,是一個反映居民消費價格水平變動情況的宏觀經濟指標.某年的![]() ,以下是
,以下是![]() 年居民消費價格指數的柱形圖.
年居民消費價格指數的柱形圖.
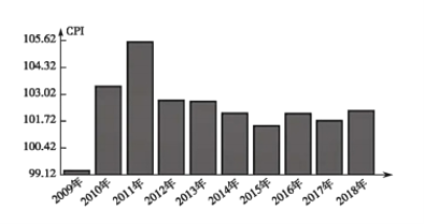
從圖中可知下列說法正確的是( )
A.![]() 年居民消費價格總體呈增長趨勢
年居民消費價格總體呈增長趨勢
B.這十年中有些年份居民消費價格增長率超過3%
C.2009年的居民消費價格出現負增長
D.2011年的居民消費價格最高
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年春季,某出租汽車公司決定更換一批新的小汽車以代替原來報廢的出租車,現有![]() 兩款車型,根據以往這兩種出租車車型的數據,得到兩款出租車車型使用壽命頻數表如下:
兩款車型,根據以往這兩種出租車車型的數據,得到兩款出租車車型使用壽命頻數表如下:
使用壽命年數 | 5年 | 6年 | 7年 | 8年 | 總計 |
| 10 | 20 | 45 | 25 | 100 |
| 15 | 35 | 40 | 10 | 100 |
(1)填寫下表,并判斷是否有![]() 的把握認為出租車的使用壽命年數與汽車車型有關?
的把握認為出租車的使用壽命年數與汽車車型有關?
使用壽命不高于 | 使用壽命不低于 | 總計 | |
| |||
| |||
總計 |
(2)司機師傅小李準備在一輛開了![]() 年的
年的![]() 型車和一輛開了
型車和一輛開了![]() 年的
年的![]() 型車中選擇,為了盡最大可能實現
型車中選擇,為了盡最大可能實現![]() 年內(含
年內(含![]() 年)不換車,試通過計算說明,他應如何選擇.
年)不換車,試通過計算說明,他應如何選擇.
附: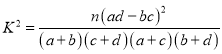 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com