
對于函數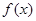 ,若在定義域存在實數
,若在定義域存在實數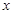 ,滿足
,滿足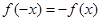 ,則稱
,則稱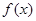 為“局部奇函數”.
為“局部奇函數”.
(1)已知二次函數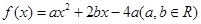 ,試判斷
,試判斷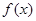 是否為“局部奇函數”?并說明理由;
是否為“局部奇函數”?并說明理由;
(2)設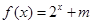 是定義在
是定義在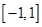 上的“局部奇函數”,求實數
上的“局部奇函數”,求實數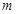 的取值范圍.
的取值范圍.
(1)是“局部奇函數”;(2)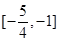 .
.
解析試題分析:(1)本題實質就是解方程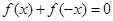 ,如果這個方程有實數解,就說明
,如果這個方程有實數解,就說明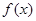 是“局部奇函數”,如果這個方程無實數解,就說明
是“局部奇函數”,如果這個方程無實數解,就說明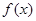 不是“局部奇函數”,易知
不是“局部奇函數”,易知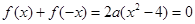 有實數解,因此答案是肯定的;(2)已經明確
有實數解,因此答案是肯定的;(2)已經明確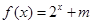 是“局部奇函數”,也就是說方程
是“局部奇函數”,也就是說方程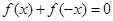 一定有實數解,問題也就變成方程
一定有實數解,問題也就變成方程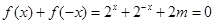 在
在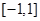 上有解,求參數
上有解,求參數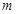 的取值范圍,又方程可變形為
的取值范圍,又方程可變形為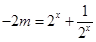 ,因此求
,因此求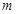 的取值范圍,就相當于求函數
的取值范圍,就相當于求函數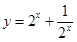
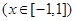 的值域,用換元法(設
的值域,用換元法(設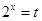 ),再借助于函數
),再借助于函數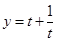 的單調性就可求出.
的單調性就可求出.
試題解析:(1)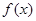 為“局部奇函數”等價于關于
為“局部奇函數”等價于關于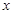 的方程
的方程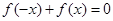 有解.
有解.
即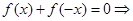
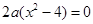 (3分)
(3分)
有解
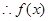 為“局部奇函數”.(5分)
為“局部奇函數”.(5分)
(2)當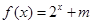 時,
時, 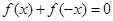 可轉化為
可轉化為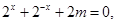 (8分)
(8分)
因為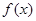 的定義域為
的定義域為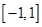 ,所以方程
,所以方程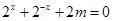 在
在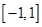 上有解,令
上有解,令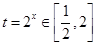 ,(9分)
,(9分)
則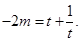
因為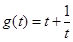 在
在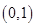 上遞減,在
上遞減,在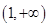 上遞增,
上遞增,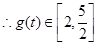 (11分)
(11分)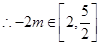 (12分)
(12分)
即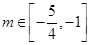 (14分)
(14分)
考點:新定義概念,方程有解求參數取值范圍問題.


科目:高中數學 來源: 題型:解答題
(12分)(2011•福建)設函數f(θ)=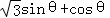 ,其中,角θ的頂點與坐標原點重合,始邊與x軸非負半軸重合,終邊經過點P(x,y),且0≤θ≤π.
,其中,角θ的頂點與坐標原點重合,始邊與x軸非負半軸重合,終邊經過點P(x,y),且0≤θ≤π.
(Ⅰ)若點P的坐標為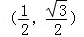 ,求f(θ)的值;
,求f(θ)的值;
(Ⅱ)若點P(x,y)為平面區域Ω: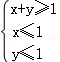 上的一個動點,試確定角θ的取值范圍,并求函數f(θ)的最小值和最大值.
上的一個動點,試確定角θ的取值范圍,并求函數f(θ)的最小值和最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了尋找馬航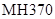 殘骸,我國“雪龍號”科考船于2014年3月26日從港口
殘骸,我國“雪龍號”科考船于2014年3月26日從港口 出發,沿北偏東
出發,沿北偏東 角的射線
角的射線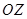 方向航行,而在港口北偏東
方向航行,而在港口北偏東 角的方向上有一個給科考船補給物資的小島
角的方向上有一個給科考船補給物資的小島 ,
,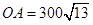 海里,且
海里,且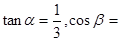
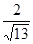 .現指揮部需要緊急征調位于港口
.現指揮部需要緊急征調位于港口 正東
正東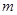 海里的
海里的 處的補給船,速往小島
處的補給船,速往小島 裝上補給物資供給科考船.該船沿
裝上補給物資供給科考船.該船沿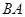 方向全速追趕科考船,并在
方向全速追趕科考船,并在 處相遇.經測算當兩船運行的航線與海岸線
處相遇.經測算當兩船運行的航線與海岸線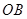 圍成的三角形
圍成的三角形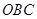 的面積
的面積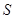 最小時,這種補給方案最優.
最小時,這種補給方案最優.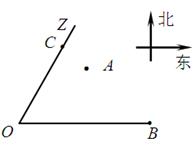
(1)求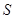 關于
關于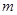 的函數關系式
的函數關系式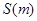 ;
;
(2)應征調位于港口正東多少海里處的補給船只,補給方案最優?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
橢圓c: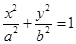 (a>b>0)的離心率為
(a>b>0)的離心率為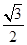 ,過其右焦點F與長軸垂直的弦長為1,
,過其右焦點F與長軸垂直的弦長為1,
(1)求橢圓C的方程;
(2)設橢圓C的左右頂點分別為A,B,點P是直線x=1上的動點,直線PA與橢圓的另一個交點為M,直線PB與橢圓的另一個交點為N,求證:直線MN經過一定點.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某廠擬在2014年通過廣告促銷活動推銷產品.經調查測算,產品的年銷售量(假定年產量=年銷售量) 萬件與年廣告費用
萬件與年廣告費用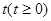 萬元滿足關系式:
萬元滿足關系式: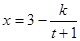 (
( 為常數).若不做廣告,則產品的年銷售量恰好為1萬件.已知2014年生產該產品時,該廠需要先固定投入8萬元,并且預計生產每1萬件該產品時,需再投入4萬元,每件產品的銷售價格定為每件產品所需的年平均成本的1.5倍(每件產品的成本包括固定投入和生產再投入兩部分,不包括廣告促銷費用).
為常數).若不做廣告,則產品的年銷售量恰好為1萬件.已知2014年生產該產品時,該廠需要先固定投入8萬元,并且預計生產每1萬件該產品時,需再投入4萬元,每件產品的銷售價格定為每件產品所需的年平均成本的1.5倍(每件產品的成本包括固定投入和生產再投入兩部分,不包括廣告促銷費用).
(1)將2014年該廠的年銷售利潤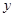 (萬元)表示為年廣告促銷費用
(萬元)表示為年廣告促銷費用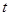 (萬元)的函數;
(萬元)的函數;
(2)2014年廣告促銷費用投入多少萬元時,該廠將獲利最大?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設f(x)=|lg x|,a,b為實數,且0<a<b.
(1)求方程f(x)=1的解;
(2)若a,b滿足f(a)=f(b)=2f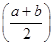 ,
,
求證:a·b=1,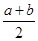 >1.
>1.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com