
【題目】已知函數![]() .
.
(1)若![]() 的最大值為
的最大值為![]() ,求
,求![]() 的值;
的值;
(2)若存在實數![]() 且
且![]() ,使得
,使得![]() ,求證:
,求證:![]() .
.
【答案】(1)![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】
(1)對函數進行求導,然后根據![]() 的正負性進行分類討論求出函數的單調性,最后根據題意求出
的正負性進行分類討論求出函數的單調性,最后根據題意求出![]() 的值;
的值;
(2)根據題意和(1)可以判斷出函數的單調性,進而可以確定![]() 介于
介于![]() 之間,不妨設
之間,不妨設![]() ,這樣根據函數的單調性和絕對值的性質進行求解即可.
,這樣根據函數的單調性和絕對值的性質進行求解即可.
(1)![]() ,若
,若![]() ,則
,則![]() ,所以
,所以![]() 在
在![]() 上單調遞增,
上單調遞增,![]() 無最值,不合題意;若
無最值,不合題意;若![]() ,當
,當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,故
上單調遞減,故![]() 的最大值
的最大值![]() ,解得
,解得![]() ,符合題意.
,符合題意.
綜上,![]() .
.
(2)若![]() ,則由(1)知
,則由(1)知![]() ,所以函數
,所以函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.若存在實數
上單調遞減.若存在實數![]() ,使得
,使得![]() ,則
,則![]() 介于
介于![]() 之間,不妨設
之間,不妨設![]() ,因為
,因為![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,且
上單調遞減,且![]() ,所以當
,所以當![]() 時,
時,![]() ,由
,由![]() ,可得
,可得![]() ,故
,故![]() ,又
,又![]() 在
在![]() 上遞增,且
上遞增,且![]() ,
,
所以![]() ,所以
,所以![]() ,
,
同理![]() .所以
.所以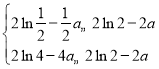 ,解得
,解得![]() ,不等式得證.
,不等式得證.


科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形![]() 是菱形,
是菱形,![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,
, ![]() ,
,![]() 為
為![]() 的中點.
的中點.
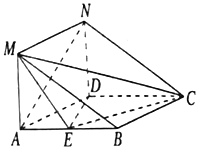
(1)平面![]() 平面
平面![]()
(2)在線段![]() 上是否存在點
上是否存在點![]() ,使二面角
,使二面角![]() 的大小為
的大小為![]() ?若存在,求出
?若存在,求出![]() 的長度;若不存在,請說明理由.
的長度;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】猜商品的價格游戲, 觀眾甲: ![]() 主持人:高了! 觀眾甲:
主持人:高了! 觀眾甲: ![]() 主持人:低了! 觀眾甲:
主持人:低了! 觀眾甲: ![]() 主持人:高了! 觀眾甲:
主持人:高了! 觀眾甲: ![]() 主持人:低了! 觀眾甲:
主持人:低了! 觀眾甲: ![]() 主持人:低了! 則此商品價格所在的區間是 ( )
主持人:低了! 則此商品價格所在的區間是 ( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以原點為極點,x軸的正半軸為極軸建立極坐標系,已知曲線![]() ,直線l的參數方程為:
,直線l的參數方程為:![]() (t為參數),直線l與曲線C分別交于
(t為參數),直線l與曲線C分別交于![]() 兩點.
兩點.
(1)寫出曲線C和直線l的普通方程;
(2)若點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的曲線圖是2020年1月25日至2020年2月12日陜西省及西安市新冠肺炎累計確診病例的曲線圖,則下列判斷正確的是( )
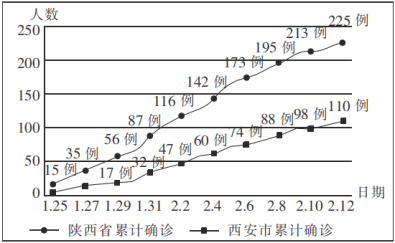
A.1月31日陜西省新冠肺炎累計確診病例中西安市占比超過了![]()
B.1月25日至2月12日陜西省及西安市新冠肺炎累計確診病例都呈遞增趨勢
C.2月2日后到2月10日陜西省新冠肺炎累計確診病例增加了97例
D.2月8日到2月10日西安市新冠肺炎累計確診病例的增長率大于2月6日到2月8日的增長率
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年3月,各行各業開始復工復產,生活逐步恢復常態,某物流公司承擔從甲地到乙地的蔬菜運輸業務.已知該公司統計了往年同期200天內每天配送的蔬菜量X(40≤X<200,單位:件.注:蔬菜全部用統一規格的包裝箱包裝),并分組統計得到表格如表:
蔬菜量X | [40,80) | [80,120) | [120,160) | [160,200) |
天數 | 25 | 50 | 100 | 25 |
若將頻率視為概率,試解答如下問題:
(1)該物流公司負責人決定隨機抽出3天的數據來分析配送的蔬菜量的情況,求這3天配送的蔬菜量中至多有2天小于120件的概率;
(2)該物流公司擬一次性租賃一批貨車專門運營從甲地到乙地的蔬菜運輸.已知一輛貨車每天只能運營一趟,每輛貨車每趟最多可裝載40件,滿載才發車,否則不發車.若發車,則每輛貨車每趟可獲利2000元;若未發車,則每輛貨車每天平均虧損400元.為使該物流公司此項業務的營業利潤最大,該物流公司應一次性租賃幾輛貨車?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若無窮數列![]() 滿足:只要
滿足:只要![]() ,必有
,必有![]() ,則稱
,則稱![]() 具有性質
具有性質![]() .
.
(1)若![]() 具有性質
具有性質![]() ,且
,且![]()
![]() ,求
,求![]() ;
;
(2)若無窮數列![]() 是等差數列,無窮數列
是等差數列,無窮數列![]() 是等比數列,
是等比數列,![]() ,
,![]() ,
,![]() .判斷
.判斷![]() 是否具有性質
是否具有性質![]() ,并說明理由;
,并說明理由;
(3)設![]() 是無窮數列,已知
是無窮數列,已知![]() .求證:“對任意
.求證:“對任意![]() 都具有性質
都具有性質![]() ”的充要條件為“
”的充要條件為“![]() 是常數列”.
是常數列”.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com