
【題目】已知函數![]() (
(![]() 為常數,
為常數,![]() ).
).
(1)討論函數![]() 的單調區間;
的單調區間;
(2)當![]() 時,若函數
時,若函數![]() 在
在![]() (
(![]() ,
,![]() 是自然對數的底數)上有兩個零點,求
是自然對數的底數)上有兩個零點,求![]() 的最小值.
的最小值.
【答案】見解析
【解析】(1)函數![]() 的定義域為R,由
的定義域為R,由![]() ,得
,得![]() . ...............2分
. ...............2分
①當![]()
![]()
![]() ,當
,當![]()
![]() ,
,![]() 的變化如下表:
的變化如下表:
|
| 0 |
|
| + | 0 | _ |
| 增 | 極大值 | 減 |
此時,![]() 的遞增區間為
的遞增區間為![]()
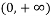
②當![]()
![]() .由
.由![]() ,得
,得![]()
![]()
![]()
![]() ,
,![]() 的變化如下表:
的變化如下表:
|
| 0 |
|
|
|
| + | 0 | - | 0 | + |
| 增 | 極大值 | 減 | 極小值 | 增 |
此時,![]() 的遞增區間為
的遞增區間為![]()
![]()
![]()
③當![]()
![]() .此時,
.此時,![]() 的遞增區間為
的遞增區間為![]()
④當![]()
![]() .由
.由![]() ,得
,得![]()
![]()
![]()
![]() ,
,![]() 的變化如下表:.
的變化如下表:.
|
|
|
| 0 |
|
| + | 0 | - | 0 | + |
| 增 | 極大值 | 減 | 極小值 | 增 |
此時,![]() 的遞增區間為
的遞增區間為![]()
![]()
![]()
綜上所述,當![]()
![]() 的遞增區間為
的遞增區間為![]()
![]()
當![]()
![]() 的遞增區間為
的遞增區間為![]()
![]()
![]()
當![]()
![]() 的遞增區間為
的遞增區間為![]()
當![]()
![]() 的遞增區間為
的遞增區間為![]()
![]()
![]()
(2)當![]() 時,
時,![]() .由(1)可知,
.由(1)可知,![]() 在
在![]()
且![]() 的極大值為
的極大值為![]() ,所以
,所以![]() 在
在![]()
![]()
由![]() ,且
,且![]() 在
在![]()
![]() . ................9分
. ................9分
要想函數![]() 在
在![]() 上還有一個零點,同時考慮到函數
上還有一個零點,同時考慮到函數![]() 在
在![]()
則只需![]() ,且
,且![]() .又因為
.又因為![]()
且![]()
![]() ,
,
所以當![]()
![]() 在
在![]() 還有一個零點,則
還有一個零點,則![]()
綜上所述,若![]() 在
在![]() 上有兩個零點時,
上有兩個零點時,![]()


 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:高中數學 來源: 題型:
【題目】已知向量![]() ,
, ![]() ,設函數
,設函數![]() ,且
,且![]() 的圖象過點
的圖象過點![]() 和點
和點![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)將![]() 的圖象向左平移
的圖象向左平移![]() (
(![]() )個單位后得到函數
)個單位后得到函數![]() 的圖象.若
的圖象.若![]() 的圖象上各最高點到點
的圖象上各最高點到點![]() 的距離的最小值為1,求
的距離的最小值為1,求![]() 的單調增區間.
的單調增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐S ABCD中,平面SAD⊥平面ABCD.四邊形ABCD為正方形,且點P為AD的中點,點Q為SB的中點.

(1)求證:CD⊥平面SAD.
(2)求證:PQ∥平面SCD.
(3)若SA=SD,點M為BC的中點,在棱SC上是否存在點N,使得平面DMN⊥平面ABCD?若存在,請說明其位置,并加以證明;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,且A,B,C成等差數列
(1)若b=2 ![]() ,c=2,求△ABC的面積;
,c=2,求△ABC的面積;
(2)若a,b,c成等比數列,試判斷△ABC的形狀.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,一個動圓截直線![]() 和
和![]() 所得的弦長分別為8,4.
所得的弦長分別為8,4.
(1)求動圓圓心的軌跡方程![]() ;
;
(2)在軌跡![]() 上是否存在這樣的點:它到點
上是否存在這樣的點:它到點![]() 的距離等于到點
的距離等于到點![]() 的距離?若存在,求出這樣的點的坐標;若不存在,說明理由.
的距離?若存在,求出這樣的點的坐標;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com