
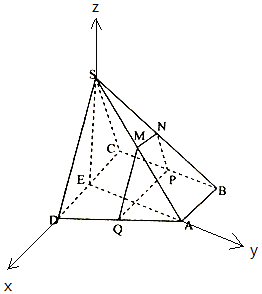
【題目】如圖,四棱錐S﹣ABCD中,底面ABCD為直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=SD=CD=AD=2AB,M,N分別為SA,SB的中點,E為CD中點,過M,N作平面MNPQ分別與BC,AD交于點P,Q,若 ![]() =t
=t ![]() .
. 
(1)當t= ![]() 時,求證:平面SAE⊥平面MNPQ;
時,求證:平面SAE⊥平面MNPQ;
(2)是否存在實數t,使得二面角M﹣PQ﹣A的平面角的余弦值為 ![]() ?若存在,求出實數t的值;若不存在,說明理由.
?若存在,求出實數t的值;若不存在,說明理由.
【答案】
(1)證明:(1)E為CD中點,∴四邊形ABCE為矩形,
∴AE⊥CD,
當t= ![]() 時,Q為AD中點,PQ∥CD,所以PQ⊥AE,
時,Q為AD中點,PQ∥CD,所以PQ⊥AE,
∵平面SCD⊥平面ABCD,SE⊥CD,∴SE⊥面ABCD,
∵PQ面ABCD,∴PQ⊥SE,∴PQ⊥面SAE,
所以面MNPQ⊥面SAE
(2)解:如圖,以E為原點,ED,EA,ES直線分別為x軸,y軸,z軸建立如圖所示坐標系;
設ED=a,則M((1﹣t)a,( ![]() ﹣
﹣ ![]() )a,
)a, ![]() a),E(0,0,0),A(0,
a),E(0,0,0),A(0, ![]() ,0),
,0),
Q((1﹣t)a, ![]() ,0),
,0), ![]() =(0,
=(0, ![]() ,
, ![]() ),
),
面ABCD一個方向向量為 ![]() =(1,0,0),
=(1,0,0),
設平面MPQ的法向量 ![]() =(x,y,z),
=(x,y,z),
則  ,取z=2,得
,取z=2,得 ![]() =(0,
=(0, ![]() ,2),
,2),
平面ABCD的法向量為 ![]() =(0,0,1)
=(0,0,1)
∵二面角M﹣PQ﹣A的平面角的余弦值為 ![]() ,
,
∴由題意:cosθ= ![]() =
= 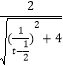 =
= ![]() ,
,
解得t= ![]() 或t=
或t= ![]() ,
,
由圖形知,當t= ![]() 時,二面角M﹣PQ﹣A為鈍二面角,不合題意,舍去
時,二面角M﹣PQ﹣A為鈍二面角,不合題意,舍去
綜上:t= ![]() .
.
【解析】(1)推導出AE⊥CD,PQ⊥AE,從而SE⊥面ABCD,由此能證明面MNPQ⊥面SAE.(2)以E為原點,ED,EA,ES直線分別為x軸,y軸,z軸建立空間直角坐標系,利用向量法能求出t的值.


 小博士期末闖關100分系列答案
小博士期末闖關100分系列答案 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)我們把一系列向量![]() 按次序排成一列,稱之為向量列,記作
按次序排成一列,稱之為向量列,記作![]() ,已知向量列
,已知向量列![]() 滿足:
滿足:![]() ,
,![]()
![]() .
.
(1)證明:數列![]() 是等比數列;
是等比數列;
(2)設![]() 表示向量
表示向量![]() 與
與![]() 間的夾角,若
間的夾角,若![]() ,對于任意正整數
,對于任意正整數![]() ,不等式
,不等式 恒成立,求實數
恒成立,求實數![]() 的范圍
的范圍
(3)設![]() ,問數列
,問數列![]() 中是否存在最小項?若存在,求出最小項;若不存在,請說明理由
中是否存在最小項?若存在,求出最小項;若不存在,請說明理由
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=. ![]() ,直線x=0,x=e,y=0,y=1所圍成的區域為M,曲線y=f(x)與直線y=1圍成的區域為N,在區域M內任取一個點P,則點P在區域N內概率為( )
,直線x=0,x=e,y=0,y=1所圍成的區域為M,曲線y=f(x)與直線y=1圍成的區域為N,在區域M內任取一個點P,則點P在區域N內概率為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,“共享單車”的出現為市民“綠色出行”提供了極大的方便,某共享單車公司“Mobike”計劃在甲、乙兩座城市共投資120萬元,根據行業規定,每個城市至少要投資40萬元,由前期市場調研可知:甲城市收益![]() 與投入
與投入![]() (單位:萬元)滿足
(單位:萬元)滿足![]() ,乙城市收益
,乙城市收益![]() 與投入
與投入![]() (單位:萬元)滿足
(單位:萬元)滿足![]() ,設甲城市的投入為
,設甲城市的投入為![]() (單位:萬元),兩個城市的總收益為
(單位:萬元),兩個城市的總收益為![]() (單位:萬元).
(單位:萬元).
(1)當甲城市投資50萬元時,求此時公司總收益;
(2)試問如何安排甲、乙兩個城市的投資,才能使總收益最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,以原點O為極點,x軸的正半軸為極軸,建立極坐標系,曲線C1的參數方程為 ![]() (θ為參數),曲線 C2的極坐標方程為ρcosθ﹣
(θ為參數),曲線 C2的極坐標方程為ρcosθ﹣ ![]() ρsinθ﹣4=0.
ρsinθ﹣4=0.
(1)求曲線C1的普通方程和曲線 C2的直角坐標方程;
(2)設P為曲線C1上一點,Q為曲線 C2上一點,求|PQ|的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是由正整數構成的數表,用![]() 表示第
表示第![]() 行第
行第![]() 個數(
個數(![]() ). 此表中
). 此表中![]() ,每行中除首尾兩數外,其他各數分別等于其“肩膀”上的兩數之和.
,每行中除首尾兩數外,其他各數分別等于其“肩膀”上的兩數之和.

(1)寫出數表的第6行(從左至右依次列出);
(2)設第![]() 行的第二個數為
行的第二個數為![]() ,求
,求![]() ;
;
(3)令![]() ,記
,記![]() 為數列
為數列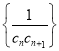 前
前![]() 項和,求
項和,求![]() 的最大值,并求此時
的最大值,并求此時![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設z1 , z2是復數,給出下列四個命題:
①若|z1﹣z2|=0,則 ![]() =
= ![]() ②若z1=
②若z1= ![]() ,則
,則 ![]() =z2
=z2
③若|z1|=|z2|,則z1 ![]() =z2
=z2 ![]() ④若|z1|=|z2|,則z12=z22
④若|z1|=|z2|,則z12=z22
其中真命題的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知公差不為0的等差數列{an}的前n項和為Sn,滿足S3=a4+4,且a2,a6,a18成等比數列.
(1)求數列{an}的通項公式;
(2)設bn=![]() ,求數列{bn}的前n項和Tn.
,求數列{bn}的前n項和Tn.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com