【題目】某班從6名班干部中（其中男生4人，女生2人），任選3人參加學校的義務勞動．
（1）設所選3人中女生人數為ξ，求ξ的分布列；
（2）求男生甲或女生乙被選中的概率．
【答案】（1）詳見解析；（2）
。
【解析】
試題分析：（1）根據題意，所選3人中女生人數
的所有可能取值為0,1,2三種，
，
，
，寫出分布列即可；
（2）從6名班干部中任選3人共用
種選法，若男生甲被選中，則有
種，若女生乙被選中，則有
種，男生甲被選中的時候包含女生乙被選中，女生乙被選中的時候也包含男生甲被選中的情況，所有男生甲或女生乙被選中的種數應為
，設男生甲或女生乙被選中為事件A，則事件A的概率為
。或者也可以求出男生甲和女生乙都不被選中的種數為
種，概率為
，根據對立事件的概率，可知男生甲或女生乙被選中的概率為
。
試題解析：（1） ξ的所有可能取值為0,1,2
依題意得
ξ | 0 | 1 | 2 |
P |
所以ξ的分布列為
（2）設“甲、乙都不被選中”為事件C
則P（C）＝＝＝
所求概率為
1－＝.
科目：高中數學 來源： 題型：
【題目】閱讀：
已知
、
，
，求
的最小值.
解法如下：
，
當且僅當
，即
時取到等號，
則的最小值為
.
應用上述解法，求解下列問題：
（1）已知
，
，求
的最小值；
（2）已知
，求函數
的最小值；
（3）已知正數
、
、
，
，
求證：
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市居民自來水收費標準如下：每戶每月用水不超過5噸時，每噸為
元，當用水超過5噸時，超過部分每噸4元。某月甲、乙兩戶共交水費
元，已知甲、乙兩戶該月用水量分別為
噸。
(1)求
關于
的函數。
(2)若甲、乙兩戶該月共交水費
元，分別求甲、乙兩戶該月的用水量和水費。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知定義在R上的函數
是奇函數,函數
的定義域為
.
（1）求
的值；
（2）若
在
上單調遞減，根據單調性的定義求實數
的取值范圍；
（3）在(2)的條件下，若函數
在區間
上有且僅有兩個不同的零點，求實數的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從某企業生產的某種產品中抽取500件，測量這些產品的一項質量指標值，由測量結果得如下頻率分布直方圖：
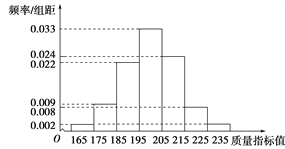
(1)求這500件產品質量指標值的樣本平均數
和樣本方差s2(同一組中的數據用該組區間的中點值作代表)；
(2)由直方圖可以認為，這種產品的質量指標值Z服從正態分布N(μ，σ2)，其中μ近似為樣本平均數
，σ2近似為樣本方差s2.
(ⅰ)利用該正態分布，求P(187.8<Z<212.2)；
(ⅱ)某用戶從該企業購買了100件這種產品，記X表示這100件產品中質量指標值位于區間(187.8，212.2)的產品件數.利用(ⅰ)的結果，求E(X).
附： 
≈12.2.若Z～N(μ，σ2)，則P(μ－σ<Z<μ＋σ)＝0.682 6，P(μ－2σ<Z<μ＋2σ)＝0.954 4.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某水果店購進某種水果的成本為
，經過市場調研發現，這種水果在未來30天的銷售單價
與時間
之間的函數關系式為
，銷售量
與時間
的函數關系式為
。
（Ⅰ）該水果店哪一天的銷售利潤最大？最大利潤是多少？
（Ⅱ）為響應政府“精準扶貧”號召，該店決定每銷售
水果就捐贈
元給“精準扶貧”對象．欲使捐贈后不虧損，且利潤隨時間
的增大而增大，求捐贈額
的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
