【題目】已知定義在R上的函數
滿足
， 
，設
與
圖象的交點坐標為
，若
，則
的最小值為____．
【答案】2
【解析】
由已知可得f（x）和h（x）的圖象均關于（a，b）對稱，故每一組對稱點有橫坐標和為2a，縱坐標和為2b，進而可得a+b=2，結合二次函數的圖象和性質，可得答案．
∵f（2a﹣x）=2b﹣f（x），可知f（x）的圖象關于（a，b）對稱，
又∵h（x+a）=
=b+
設g（x）=，則g（﹣x）=﹣g（x），即g（x）為奇函數，
∴y=h（x）的圖象關于（a，b）對稱，
∴對于每一組對稱點有橫坐標和為2a，縱坐標和為2b，
∴
（xi+yi）=2am+2bm=4m，
∴a+b=2，
故a2+b2=a2+（2﹣a）2=2a2﹣4a+4=2（a﹣1）2+2≥2
當且僅當a=b=1時，a2+b2取最小值2．
故答案為：2．
科目：高中數學 來源： 題型：
【題目】為響應國家提出的“大眾創業，萬眾創新”的號召,小李同學大學畢業后,決定利用所學專業進行自主創業。經過市場調查,生產某小型電子產品需投入年固定成本為5萬元，每年生產
萬件，需另投入流動成本為
萬元，且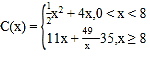
，每件產品售價為10元。經市場分析,生產的產品當年能全部售完。
(1)寫出年利潤
(萬元)關于年產量(萬件)的函數解析式；
(注:年利潤=年銷售收入-固定成本-流動成本)
(2)年產量為多少萬件時，小李在這一產品的生產中所獲利潤最大?最大利潤是多少?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“微信運動”是一個類似計步數據庫的公眾賬號.用戶只需以運動手環或手機協處理器的運動數據為介，然后關注該公眾號，就能看見自己與好友每日行走的步數，并在同一排行榜上得以體現.現隨機選取朋友圈中的50人，記錄了他們某一天的走路步數，并將數據整理如下：
步數/步 |
|
|
|
| 10000以上 |
男生人數/人 | 1 | 2 | 7 | 15 | 5 |
女性人數/人 | 0 | 3 | 7 | 9 | 1 |
規定：人一天行走的步數超過8000步時被系統評定為“積極性”，否則為“懈怠性”.
（1）填寫下面列聯表（單位：人），并根據列表判斷是否有90%的把握認為“評定類型與性別有關”；
積極性 | 懈怠性 | 總計 | |
男 | |||
女 | |||
總計 |
附：
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
（2）為了進一步了解“懈怠性”人群中每個人的生活習慣，從步行數在
的人群中再隨機抽取3人，求選中的人中男性人數超過女性人數的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左、右頂點分別為
，
，且以線段
為直徑的圓與直線
相切，橢圓
截直線
所得線段的長度為1.
（1）求橢圓的方程；
（2）設過點
的動直線
與橢圓相交于
，
兩點，若
（
為坐標原點），求直線的斜率的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，點
，直線
：
，圓
：
.
（1）求
的取值范圍，并求出圓心坐標；
（2）若圓的半徑為1，過點
作圓的切線，求切線的方程；
（3）有一動圓
的半徑為1，圓心在上，若動圓上存在點
，使
，求圓心的橫坐標
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓C經過A（5，3），B（4，4）兩點，且圓心在x軸上.
（1）求圓C的標準方程；
（2）若直線l過點（5，2），且被圓C所截得的弦長為6，求直線l的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
