
【題目】函數(shù)![]() ,
,![]() .
.
(Ⅰ)討論![]() 的極值點的個數(shù);
的極值點的個數(shù);
(Ⅱ)若對于![]() ,總有
,總有![]() .(i)求實數(shù)
.(i)求實數(shù)![]() 的范圍; (ii)求證:對于
的范圍; (ii)求證:對于![]() ,不等式
,不等式![]() 成立.
成立.
【答案】見解析.
【解析】【試題分析】(Ⅰ)先運用求導(dǎo)法則求函數(shù)的導(dǎo)數(shù),再分類進行探求; (Ⅱ)先將不等式進行等價轉(zhuǎn)化,再構(gòu)造函數(shù)借助導(dǎo)數(shù)的有關(guān)知識進行推證:
(Ⅰ)解法一:由題意得![]() , 令
, 令![]()
(1)當(dāng)![]() ,即
,即![]() 時,
時,![]() 對
對![]() 恒成立
恒成立
即![]() 對
對![]() 恒成立,此時
恒成立,此時![]() 沒有極值點;…………2分
沒有極值點;…………2分
(2)當(dāng)![]() ,即
,即![]()
①![]() 時,設(shè)方程
時,設(shè)方程![]() 兩個不同實根為
兩個不同實根為![]() ,不妨設(shè)
,不妨設(shè)![]()
則![]() ,故
,故![]()
∴![]() 時
時![]() ;在
;在![]() 時
時![]()
故![]() 是函數(shù)
是函數(shù)![]() 的兩個極值點.
的兩個極值點.
②![]() 時,設(shè)方程
時,設(shè)方程![]() 兩個不同實根為
兩個不同實根為![]() ,
,
則![]() ,故
,故![]()
∴![]() 時,
時,![]() ;故函數(shù)
;故函數(shù)![]() 沒有極值點. ……………………………4分
沒有極值點. ……………………………4分
綜上,當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 有兩個極值點;
有兩個極值點;
當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 沒有極值點. ………………………………………5分
沒有極值點. ………………………………………5分
解法二:![]() , …………………………………………1分
, …………………………………………1分
![]() ,
,
![]() 當(dāng)
當(dāng)![]() ,即
,即![]() 時,
時,![]() 對
對![]() 恒成立,
恒成立,![]() 在
在![]() 單調(diào)增,
單調(diào)增,![]() 沒有極值點; ……………………………………………………………3分
沒有極值點; ……………………………………………………………3分
②當(dāng)![]() ,即
,即![]() 時,方程
時,方程![]() 有兩個不等正數(shù)解
有兩個不等正數(shù)解![]() ,
,
![]()
不妨設(shè)![]() ,則當(dāng)
,則當(dāng)![]() 時,
時,![]() 增;
增;![]() 時,
時,![]() 減;
減;![]() 時,
時,![]() 增,所以
增,所以![]() 分別為
分別為![]() 極大值點和極小值點,
極大值點和極小值點,![]() 有兩個極值點.
有兩個極值點.
綜上所述,當(dāng)![]() 時,
時,![]() 沒有極值點;
沒有極值點;
當(dāng)![]() 時,
時,![]() 有兩個極值點. ………………………………5分
有兩個極值點. ………………………………5分
(Ⅱ)(i)![]() ,
,
由![]() ,即
,即![]() 對于
對于![]() 恒成立,設(shè)
恒成立,設(shè)![]() ,
,
![]() ,
,
![]() ,
,![]() 時,
時,![]() 減,
減,![]() 時,
時,![]() 增,
增,
![]() ,
,![]() . ……………………………………9分
. ……………………………………9分
(ii)由(i)知,當(dāng)![]() 時有
時有![]() ,即:
,即:![]() ,
,![]() ……①當(dāng)且僅當(dāng)
……①當(dāng)且僅當(dāng)![]() 時取等號, ……………………………10分
時取等號, ……………………………10分
以下證明:![]() ,設(shè)
,設(shè)![]() ,
,![]() ,
,
![]() 當(dāng)
當(dāng)![]() 時
時![]() 減,
減,![]() 時
時![]() 增,
增,
![]() ,
,![]() ,……②當(dāng)且僅當(dāng)
,……②當(dāng)且僅當(dāng)![]() 時取等號;
時取等號;
由于①②等號不同時成立,故有![]() .……………………………12分
.……………………………12分


科目:高中數(shù)學(xué) 來源: 題型:
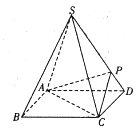
【題目】如圖,四棱錐![]() 的底面是正方形,每條側(cè)棱的長都是底面邊長的
的底面是正方形,每條側(cè)棱的長都是底面邊長的![]() 倍,P為側(cè)棱SD上的點,且
倍,P為側(cè)棱SD上的點,且![]() .
.
(1)求二面角![]() 的大小;
的大小;
(2)在側(cè)棱SC上是否存在一點E,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,試說明理由.
的值;若不存在,試說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某學(xué)校用簡單隨機抽樣方法抽取了30名同學(xué),對其每月平均課外閱讀時間(單位:小時)進行調(diào)查,莖葉圖如圖:
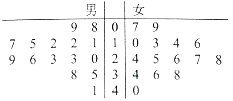
若將月均課外閱讀時間不低于30小時的學(xué)生稱為“讀書迷”.
(1)將頻率視為概率,估計該校900名學(xué)生中“讀書迷”有多少人?
(2)從已抽取的7名“讀書迷”中隨機抽取男、女“讀書迷”各1人,參加讀書日宣傳活動.
(i)共有多少種不同的抽取方法?
(ii)求抽取的男、女兩位“讀書迷”月均讀書時間相差不超過2小時的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知等差數(shù)列{an}中,前m(m為奇數(shù))項的和為77,其中偶數(shù)項之和為33,且a1﹣am=18,則數(shù)列{an}的通項公式為an= .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖是某市2017年3月1日至16日的空氣質(zhì)量指數(shù)趨勢圖,空氣質(zhì)量指數(shù)![]() 小于
小于![]() 表示空氣質(zhì)量優(yōu)良,空氣質(zhì)量指數(shù)大于
表示空氣質(zhì)量優(yōu)良,空氣質(zhì)量指數(shù)大于![]() 表示空氣重度污染.
表示空氣重度污染.
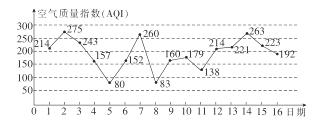
(1)若該人隨機選擇3月1日至3月14日中的某一天到達該市,到達后停留![]() 天(到達當(dāng)日算
天(到達當(dāng)日算![]() 天),求此人停留期間空氣重度污染的天數(shù)為
天),求此人停留期間空氣重度污染的天數(shù)為![]() 天的概率;
天的概率;
(2)若該人隨機選擇3月7日至3月12日中的![]() 天到達該市,求這
天到達該市,求這![]() 天中空氣質(zhì)量恰有
天中空氣質(zhì)量恰有![]() 天是重度污染的概率.
天是重度污染的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() ,
, ![]() (
(![]() ).
).
(Ⅰ)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)若函數(shù)![]() 在
在![]() 處取得極大值,求正實數(shù)
處取得極大值,求正實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義:若兩個橢圓的離心率相等,則稱兩個橢圓是“相似”的.如圖,橢圓![]() 與橢圓
與橢圓![]() 是相似的兩個橢圓,并且相交于上下兩個頂點.橢圓
是相似的兩個橢圓,并且相交于上下兩個頂點.橢圓![]() 的長軸長是4,橢圓
的長軸長是4,橢圓![]() 短軸長是1,點
短軸長是1,點![]() 分別是橢圓
分別是橢圓![]() 的左焦點與右焦點.
的左焦點與右焦點.
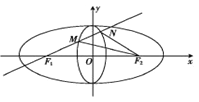
(1)求橢圓![]() 的方程;
的方程;
(2)過![]() 的直線交橢圓
的直線交橢圓![]() 于點
于點![]() ,求
,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com