
【題目】某公司為獲得較好的收益,每年要投入一定資金用于廣告促銷,經調查,每年投入廣告費![]() (百萬元),可增加銷售額約為
(百萬元),可增加銷售額約為![]() (百萬元)(
(百萬元)(![]() )
)
(1)若該公司當年的廣告費控制在4百萬元之內,則應該設入多少廣告費,才能使該公司獲得的收益最大?
(2)現該公司準備共投入6百萬元,分別用于廣告促銷售和技術改造,經預測,每設入技術改造費![]() (百萬元),可增加銷售額約為
(百萬元),可增加銷售額約為![]() (百萬元),請設計一種資金分配方案,使該公司由此獲得最大收益.(注:收益
(百萬元),請設計一種資金分配方案,使該公司由此獲得最大收益.(注:收益![]() 銷售額
銷售額![]() 成本)
成本)
【答案】(1) 該公司應該投入3百萬元用于廣告宣傳,所獲得的收益最大;(2) 該公司投資3百萬元用于廣告促銷,3百萬元用于技術改造,可以獲得最大有益.
【解析】試題分析:(1)設投入t(t百萬元)的廣告費后增加的收益為f(t)根據收益為銷售額與投放的差可建立收益模型為:f(t)=![]() ,再由二次函數法求得最大值.
,再由二次函數法求得最大值.
(2)根據題意,若用技術改造的資金為x(百萬元),則用于廣告促銷的資金為![]() (百萬元),則收益模型為:
(百萬元),則收益模型為: ![]() ,因為是高次函數,所以用導數法研究其單調性和極值,最終求得最大值.
,因為是高次函數,所以用導數法研究其單調性和極值,最終求得最大值.
(Ⅰ)廣告費![]() ,由此產生的收益
,由此產生的收益![]()
當![]() 時,
時, ![]() 最大,也即該公司應該投入3百萬元用于廣告宣傳,所獲得的收益最大.
最大,也即該公司應該投入3百萬元用于廣告宣傳,所獲得的收益最大.
(Ⅱ)設6百萬元投資中有![]() 百萬用于技術改造,
百萬用于技術改造, ![]() 百萬用于廣告宣傳,則公司由此產生的收益為
百萬用于廣告宣傳,則公司由此產生的收益為![]()
![]() ,
,
對![]() 求導數,
求導數, ![]() ,當
,當![]() 時,
時, ![]() 最大,
最大,
所以該公司投資3百萬元用于廣告促銷,3百萬元用于技術改造,可以獲得最大有益.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:
【題目】在矩形ABCD中,對角線AC與相鄰兩邊所成的角為α,β,則cos2α+cos2β=1.類比到空間中一個正確命題是:在長方體ABCD﹣A1B1C1D1中,對角線AC1與相鄰三個面所成的角為α,β,γ,則有 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設某大學的女生體重y(單位:kg)與身高x(單位:cm)具有線性相關關系,根據一組樣本數據(xi , yi)(i=1,2,…,n),用最小二乘法建立的回歸方程為 ![]() =0.85x﹣85.71,則下列結論中不正確的是( )
=0.85x﹣85.71,則下列結論中不正確的是( )
A.y與x具有正的線性相關關系
B.回歸直線過樣本點的中心( ![]() ,
, ![]() )
)
C.若該大學某女生身高增加1cm,則其體重約增加0.85kg
D.若該大學某女生身高為170cm,則可斷定其體重必為58.79kg
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,我市某居民小區擬在邊長為1百米的正方形地塊ABCD上劃出一個三角形地塊APQ種植草坪,兩個三角形地塊PAB與QAD種植花卉,一個三角形地塊CPQ設計成水景噴泉,四周鋪設小路供居民平時休閑散步,點P在邊BC上,點Q在邊CD上,記∠PAB=a. 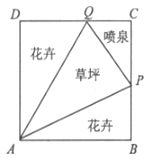
(1)當∠PAQ= ![]() 時,求花卉種植面積S關于a的函數表達式,并求S的最小值;
時,求花卉種植面積S關于a的函數表達式,并求S的最小值;
(2)考慮到小區道路的整體規劃,要求PB+DQ=PQ,請探究∠PAQ是否為定值,若是,求出此定值,若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A=[a﹣3,a],函數 ![]() (﹣2≤x≤5)的單調減區間為集合B.
(﹣2≤x≤5)的單調減區間為集合B.
(1)若a=0,求(RA)∪(RB);
(2)若A∩B=A,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,我國南海某處的一個圓形海域上有四個小島,小島B與小島A、小島C相距都為5n mile,與小島D相距為 ![]() n mile.小島A對小島B與D的視角為鈍角,且
n mile.小島A對小島B與D的視角為鈍角,且 ![]() .
.
(Ⅰ)求小島A與小島D之間的距離和四個小島所形成的四邊形的面積;
(Ⅱ)記小島D對小島B與C的視角為α,小島B對小島C與D的視角為β,求sin(2α+β)的值.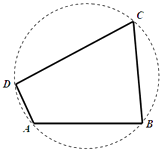
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,已知長方體ABCD﹣A1B1C1D1中,AB=BC=2,AA1=4,E是棱CC1上的點,且BE⊥B1C.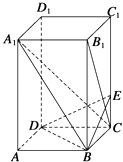
(1)求CE的長;
(2)求證:A1C⊥平面BED;
(3)求A1B與平面BDE夾角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com