
【題目】某營養(yǎng)協(xié)會對全市18歲男生的身高作調(diào)查,統(tǒng)計顯示全市18歲男生的身高服從正態(tài)分布![]() ,現(xiàn)某校隨機(jī)抽取了100名18歲男生的身高分析,結(jié)果這100名學(xué)生的身高全部介于
,現(xiàn)某校隨機(jī)抽取了100名18歲男生的身高分析,結(jié)果這100名學(xué)生的身高全部介于![]() 到
到![]() 之間.現(xiàn)將結(jié)果按如下方式分為6組,第一組
之間.現(xiàn)將結(jié)果按如下方式分為6組,第一組![]() ,第二組
,第二組![]() ,…,第六組
,…,第六組![]() ,得到如圖所示的頻率分布直方圖.
,得到如圖所示的頻率分布直方圖.
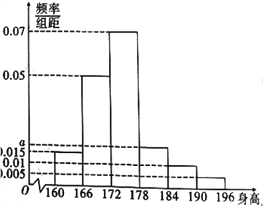
(1)若全市18歲男生共有![]() 人,試估計該市身高在
人,試估計該市身高在![]() 以上的18歲男生人數(shù);
以上的18歲男生人數(shù);
(2)求![]() 的值,并計算該校18歲男生的身高的中位數(shù)(精確到小數(shù)點(diǎn)后三位);
的值,并計算該校18歲男生的身高的中位數(shù)(精確到小數(shù)點(diǎn)后三位);
(3)若身高![]() 以上的學(xué)生校服需要單獨(dú)定制,現(xiàn)從這100名學(xué)生中身高在
以上的學(xué)生校服需要單獨(dú)定制,現(xiàn)從這100名學(xué)生中身高在![]() 以上的同學(xué)中任意抽取3人,這三人中校服需要單獨(dú)定制的人數(shù)記為
以上的同學(xué)中任意抽取3人,這三人中校服需要單獨(dú)定制的人數(shù)記為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附: ![]() ,則
,則![]() ;
;
![]() ,則
,則![]() ;
;
![]() ,則
,則![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)分布列見解析,
;(3)分布列見解析, ![]() .
.
【解析】試題分析:
(1)根據(jù)正態(tài)分布得到![]() ,故
,故![]() ,從而可得身高在
,從而可得身高在![]() 以上的18歲男生人數(shù).(2)根據(jù)頻率分布直方圖中所有小長方形的面積和為1可求得
以上的18歲男生人數(shù).(2)根據(jù)頻率分布直方圖中所有小長方形的面積和為1可求得![]() ,然后根據(jù)中位數(shù)的意義可求得中位數(shù)的估計值.(3)由頻率分布直方圖可得身高在
,然后根據(jù)中位數(shù)的意義可求得中位數(shù)的估計值.(3)由頻率分布直方圖可得身高在![]() 內(nèi)的為
內(nèi)的為![]() 人,身高在
人,身高在![]() 內(nèi)的為
內(nèi)的為![]() 人.從而可得隨機(jī)變量
人.從而可得隨機(jī)變量![]() 的所有可能取值,并根據(jù)古典概型求得對應(yīng)的概率,于是可得分布列,從而可得期望.
的所有可能取值,并根據(jù)古典概型求得對應(yīng)的概率,于是可得分布列,從而可得期望.
試題解析:
(1)由題意得![]() ,
,
∴![]() ,
,
∴可估計該市身高在![]() 以上的18歲男生人數(shù)為
以上的18歲男生人數(shù)為![]() (人)
(人)
(2)由頻率分布直方圖可得![]() ,
,
∴![]() .
.
設(shè)中位數(shù)為![]() ,則
,則![]() ,
,
∴![]() .
.
即中位數(shù)為![]() .
.
(3)由題意得身高在![]() 內(nèi)的人數(shù)為
內(nèi)的人數(shù)為![]() 人,
人,
身高在![]() 內(nèi)的人數(shù)為
內(nèi)的人數(shù)為![]() 人,
人,
由題意得隨機(jī)變量![]() 的所有可能取值為0,1,2,3.
的所有可能取值為0,1,2,3.
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
故![]() 的分布列如下:
的分布列如下:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
∴![]() .
.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知向量![]() ,
,![]() ,
,![]() ,
,![]() ,函數(shù)
,函數(shù)![]() ,
,![]() 的最小正周期為
的最小正周期為![]() .
.
(1)求![]() 的單調(diào)增區(qū)間;
的單調(diào)增區(qū)間;
(2)方程![]() ;在
;在![]() 上有且只有一個解,求實(shí)數(shù)n的取值范圍;
上有且只有一個解,求實(shí)數(shù)n的取值范圍;
(3)是否存在實(shí)數(shù)m滿足對任意x1∈[-1,1],都存在x2∈R,使得![]() +
+![]() +m(
+m(![]() -
-![]() )+1>f(x2)成立.若存在,求m的取值范圍;若不存在,說明理由.
)+1>f(x2)成立.若存在,求m的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某商場舉行購物抽獎活動,抽獎箱中放有編號分別為![]() 的五個小球.小球除編號不同外,其余均相同.活動規(guī)則如下:從抽獎箱中隨機(jī)抽取一球,若抽到的小球編號為
的五個小球.小球除編號不同外,其余均相同.活動規(guī)則如下:從抽獎箱中隨機(jī)抽取一球,若抽到的小球編號為![]() ,則獲得獎金
,則獲得獎金![]() 元;若抽到的小球編號為偶數(shù),則獲得獎金
元;若抽到的小球編號為偶數(shù),則獲得獎金![]() 元;若抽到其余編號的小球,則不中獎.現(xiàn)某顧客依次有放回的抽獎兩次.
元;若抽到其余編號的小球,則不中獎.現(xiàn)某顧客依次有放回的抽獎兩次.
(1)求該顧客兩次抽獎后都沒有中獎的概率;
(2)求該顧客兩次抽獎后獲得獎金之和為![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】盒中共有9個球,其中有4個紅球、3個黃球和2個綠球,這些球除顏色外完全相同.
(1)從盒中一次隨機(jī)取出2個球,求取出的2個球的顏色相同的概率P;
(2)從盒中一次隨機(jī)取出4個球,其中紅球、黃球、綠球的個數(shù)分別記為x1,x2,x3,隨機(jī)變量X表示x1,x2,x3中的最大數(shù),求X的概率分布和數(shù)學(xué)期望E(X).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的部分圖象如圖所示,則下列判斷正確的是( )
的部分圖象如圖所示,則下列判斷正確的是( )

A. 函數(shù)的圖象關(guān)于點(diǎn)![]() 對稱
對稱
B. 函數(shù)的圖象關(guān)于直線![]() 對稱
對稱
C. 函數(shù)![]() 的最小正周期為
的最小正周期為![]()
D. 當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 的圖象與直線
的圖象與直線![]() 圍成的封閉圖形面積為
圍成的封閉圖形面積為![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ).
).
(1)若![]() 時,
時, ![]() 不單調(diào),求
不單調(diào),求![]() 的取值范圍;
的取值范圍;
(2)設(shè)![]() ,若
,若![]() ,
, ![]() 時,
時, ![]() 時,
時, ![]() 有最小值,求最小值的取值范圍.
有最小值,求最小值的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了調(diào)查甲、乙兩個網(wǎng)站受歡迎的程度,隨機(jī)選取了14天,統(tǒng)計上午8:00-10:00間各自的點(diǎn)擊量:
甲:73,24,58,72,64,38,66,70,20,41,55,67,8,25
乙:12,37,21,5,54,42,61,45,19,6,71,36,42,14
(1)請用莖葉圖表示上面的數(shù)據(jù).
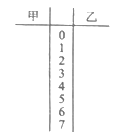
(2)甲網(wǎng)站點(diǎn)擊量在[10,40]間的頻率是多少?
(3)甲、乙兩個網(wǎng)站哪個更受歡迎?并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,曲線
,曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線與
處的切線與![]() 軸平行.函數(shù)
軸平行.函數(shù)![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求證:函數(shù)![]() 共有兩個零點(diǎn),一個零點(diǎn)是
共有兩個零點(diǎn),一個零點(diǎn)是![]() ,另一個零點(diǎn)
,另一個零點(diǎn)![]() 在區(qū)間
在區(qū)間![]() 內(nèi);
內(nèi);
(Ⅲ)求證:存在![]() ,當(dāng)
,當(dāng)![]() 時,
時, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點(diǎn)分別為
的兩個焦點(diǎn)分別為![]() ,且橢圓
,且橢圓![]() 經(jīng)過點(diǎn)
經(jīng)過點(diǎn)![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設(shè)過點(diǎn)![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 、
、![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 是線段
是線段![]() 上的點(diǎn),且
上的點(diǎn),且![]() ,求點(diǎn)
,求點(diǎn)![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com