
【題目】某校進行理科、文科數學成績對比,某次考試后,各隨機抽取100名同學的數學考試成績進行統計,其頻率分布表如下.
分組 | 頻數 | 頻率 | 分組 | 頻數 | 頻率 | |
[135,150] | 8 | 0.08 | [135,150] | 4 | 0.04 | |
[120,135) | 17 | 0.17 | [120,135) | 18 | 0.18 | |
[105,120) | 40 | 0.4 | [105,120) | 37 | 0.37 | |
[90,105) | 21 | 0.21 | [90,105) | 31 | 0.31 | |
[75,90) | 12 | 0. 12 | [75,90) | 7 | 0.07 | |
[60,75) | 2 | 0.02 | [60,75) | 3 | 0.03 | |
總計 | 100 | 1 | 總計 | 100 | 1 |
理科 文科
(Ⅰ)根據數學成績的頻率分布表,求文科數學成績的中位數的估計值;(精確到0.01)
(Ⅱ)請填寫下面的列聯表,并根據列聯表判斷是否有90%的把握認為數學成績與文理科有關:
數學成績 | 數學成績<120分 | 合計 | |
理科 | |||
文科 | |||
合計 | 200 |
參考公式與臨界值表: ![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 | |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
【答案】(Ⅰ)108.65分(Ⅱ)沒有90%的把握認為數學成績與文理科有關
【解析】分析:(Ⅰ)由圖表求出理科數學成績的頻率分布表中成績小于105分的頻率和成績大于120分的頻率,由![]() 得答案;
得答案;
(Ⅱ)根據題目所給的數據填寫2×2列聯表即可,計算K的觀測值K2,對照題目中的表格,得出統計結論.
詳解:(Ⅰ)文科數學成績的頻率分布表中,成績小于105分的頻率為0.41<0.5,
成績小于120分的頻率為0.78>0.5,
故文科數學成績的中位數的估計值為![]() 分.
分.
(Ⅱ)根據數學成績的頻率分布表得如下列聯表:
數學成績 | 數學成績 | 合計 | |
理科 | 25 | 75 | 100 |
文科 | 22 | 78 | 100 |
合計 | 47 | 153 | 200 |
![]() ,故沒有90%的把握認為數學成績與文理科有關.
,故沒有90%的把握認為數學成績與文理科有關.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】設Sn為數列{an}的前n項和,已知![]() ,對任意n∈N*,都有2Sn=(n+1)an.
,對任意n∈N*,都有2Sn=(n+1)an.
(1)求數列{an}的通項公式;
(2)若數列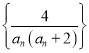 的前項和為Tn,求Tn的取值范圍.
的前項和為Tn,求Tn的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三點![]() ,
,![]() ,
,![]() ,曲線
,曲線![]() 上任意一點
上任意一點![]() 滿足
滿足![]() .
.
求![]() 的方程;
的方程;
已知點![]() ,動點
,動點![]()
![]() 在曲線C上,曲線C在Q處的切線
在曲線C上,曲線C在Q處的切線![]() 與直線PA,PB都相交,交點分別為D,E,求
與直線PA,PB都相交,交點分別為D,E,求![]() 與
與![]() 的面積的比值.
的面積的比值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖象與函數
的圖象與函數![]() 的圖象有三個不同的交點
的圖象有三個不同的交點![]() 、
、![]() 、
、![]() ,其中
,其中![]() .給出下列四個結論: ①
.給出下列四個結論: ①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中,正確結論的個數有( )個
.其中,正確結論的個數有( )個
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平行四邊形ABCD中, ![]() ,
, ![]() ,若將其沿AC折成直二面角D﹣AC﹣B,則三棱錐D﹣ACB的外接球的表面積為( )
,若將其沿AC折成直二面角D﹣AC﹣B,則三棱錐D﹣ACB的外接球的表面積為( )
A.16π
B.8π
C.4π
D.2π
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司在新年晚會上舉行抽獎活動,有甲,乙兩個抽獎方案供員工選擇. 方案甲:員工最多有兩次抽獎機會,每次抽獎的中獎率均為 ![]() ,第一次抽獎,若未中獎,則抽獎結束,若中獎,則通過拋一枚質地均勻的硬幣,決定是否繼續進行第二次抽獎,規定:若拋出硬幣,反面朝上,員工則獲得500元獎金,不進行第二次抽獎;若正面朝上,員工則須進行第二次抽獎,且在第二次抽獎中,若中獎,則獲得1000元;若未中獎,則不能獲得獎金.
,第一次抽獎,若未中獎,則抽獎結束,若中獎,則通過拋一枚質地均勻的硬幣,決定是否繼續進行第二次抽獎,規定:若拋出硬幣,反面朝上,員工則獲得500元獎金,不進行第二次抽獎;若正面朝上,員工則須進行第二次抽獎,且在第二次抽獎中,若中獎,則獲得1000元;若未中獎,則不能獲得獎金.
方案乙:員工連續三次抽獎,每次中獎率均為 ![]() ,每次中獎均可獲得獎金400元.
,每次中獎均可獲得獎金400元.
(Ⅰ)求某員工選擇方案甲進行抽獎所獲獎金X(元)的分布列;
(Ⅱ)試比較某員工選擇方案乙與選擇方案甲進行抽獎,哪個方案更劃算?
(Ⅲ)已知公司共有100人在活動中選擇了方案甲,試估計這些員工活動結束后沒有獲獎的人數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,BC=2,CD=1+![]() ,過A作AE⊥CD,垂足為E,現將△ADE沿AE折疊,使得DE⊥EC.
,過A作AE⊥CD,垂足為E,現將△ADE沿AE折疊,使得DE⊥EC.

(1)求證:BC⊥面CDE;
(2)在線段AE上是否存在一點R,使得面BDR⊥面DCB,若存在,求出點R的位置;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某學校的800名男生中隨機抽取50名測量其身高,被測學生身高全部介于![]() 和
和![]() 之間,將測量結果按如下方式分組:第一組
之間,將測量結果按如下方式分組:第一組![]() ,第二組
,第二組![]() ,…,第八組
,…,第八組![]() ,如圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組人數相同,第六組的人數為4.
,如圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組人數相同,第六組的人數為4.

(1)請補全頻率分布直方圖并求第七組的頻率;
(2)估計該校的800名男生的身高的中位數以及身高在![]() 以上(含
以上(含![]() )的人數;
)的人數;
(3)若從身高屬于第六組和第八組的所有男生中隨機抽取兩名男生,記他們的身高分別為![]() ,
,![]() ,事件
,事件![]() ,事件
,事件![]() ,求
,求![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)對任意的x∈R,都有f(﹣x)+f(x)=﹣6,且當x≥0時,f(x)=2x﹣4,定義在R上的函數g(x)=a(x﹣a)(x+a+1),兩函數同時滿足:x∈R,都有f(x)<0或g(x)<0;x∈(﹣∞,﹣1),f(x)g(x)<0,則實數a的取值范圍為( )
A.(﹣3,0)
B.![]()
C.(﹣3,﹣1)
D.(﹣3,﹣1]
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com